题目内容
11.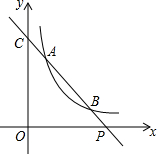 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
分析 (1)先把A(1,3)),B(3,y2)代入y=$\frac{k}{x}$求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出$\frac{CD}{OC}$=$\frac{AD}{OP}$,$\frac{PF}{PE}$=$\frac{BF}{AE}$=$\frac{PB}{PA}$,根据题意得出$\frac{1}{{y}_{1}+1}$=$\frac{{x}_{1}}{6}$,$\frac{PF}{PE}$=$\frac{BF}{AE}$=$\frac{1}{2}$,从而求得B($\frac{6+{x}_{1}}{2}$,$\frac{1}{2}$y1),然后根据k=xy得出x1•y1=$\frac{6+{x}_{1}}{2}$•$\frac{1}{2}$y1,求得x1=2,代入$\frac{1}{{y}_{1}+1}$=$\frac{{x}_{1}}{6}$,解得y1=2,即可求得A、B的坐标;
(3)合(1),(2)中的结果,猜想x1+x2=x0.
解答 解:(1)∵直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(1,3),
∴k=1×3=3,
∴y=$\frac{3}{x}$,
∵B(3,y2)在反比例函数的图象上,
∴y2=$\frac{3}{3}$=1,
∴B(3,1),
∵直线y=ax+b经过A、B两点,
∴$\left\{\begin{array}{l}{a+b=3}\\{3a+b=1}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
∴直线为y=-x+4,
令y=0,则x=4,
∴P(4,O);
(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,
则AD∥BG∥x轴,AE∥BF∥y轴,
∴$\frac{CD}{OC}$=$\frac{AD}{OP}$,$\frac{PF}{PE}$=$\frac{BF}{AE}$=$\frac{PB}{PA}$,
∵b=y1+1,AB=BP,
∴$\frac{1}{{y}_{1}+1}$=$\frac{{x}_{1}}{6}$,
$\frac{PF}{PE}$=$\frac{BF}{AE}$=$\frac{1}{2}$,
∴B($\frac{6+{x}_{1}}{2}$,$\frac{1}{2}$y1)
∵A,B两点都是反比例函数图象上的点,
∴x1•y1=$\frac{6+{x}_{1}}{2}$•$\frac{1}{2}$y1,
解得x1=2,
代入$\frac{1}{{y}_{1}+1}$=$\frac{{x}_{1}}{6}$,解得y1=2,
∴A(2,2),B(4,1).
(3)根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.
点评 本题考查了待定系数法求解析式以及反比例函数和一次函数的交点问题,数形结合思想的运用是解题的关键.

 如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )
如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )| A. | 70° | B. | 110° | C. | 30° | D. | 150° |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
 如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数 y=$\frac{m}{x}$的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数 y=$\frac{m}{x}$的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.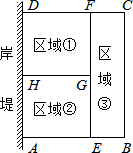 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
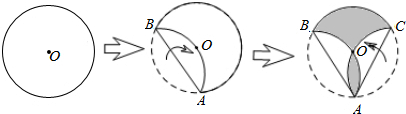
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.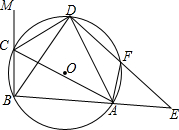 在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上-
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上- 如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.
如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点. 如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )