题目内容
3.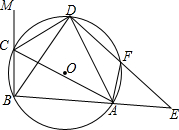 在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上-
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上-点,且$\widehat{AF}$=$\widehat{BC}$ 连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.
分析 (1)由CD是△ABC的外角平分线,可得∠MCD=∠ACD,又由∠MCD+∠BCD=180°,∠BCD+∠BAD=180°,可得∠MCD=∠BAD,继而证得∠ABD=∠BAD,即可得DB=DA;
(2)由DB=DA,可得$\widehat{DB}$=$\widehat{DA}$,即可得$\widehat{AF}$=$\widehat{BC}$,则可证得CD=FD,BC=AF,然后由SSS判定△BCD≌△AFD;
(3)首先连接DO并延长,交AB于点N,连接OB,由∠ACM=120°,易证得△ABD是等边三角形,并可求得边长,易证得△ACD∽△EBD,然后由相似三角形的对应边成比例,求得DE的长.
解答 解:(1)DB=DA.
理由:∵CD是△ABC的外角平分线,
∴∠MCD=∠ACD,
∵∠MCD+∠BCD=180°,∠BCD+∠BAD=180°,
∴∠MCD=∠BAD,
∴∠ACD=∠BAD,
∵∠ACD=∠ABD,
∴∠ABD=∠BAD,
∴DB=DA;
(2)证明:∵DB=DA,
∴$\widehat{DB}$=$\widehat{DA}$,
∵$\widehat{AF}$=$\widehat{BC}$,
∴AF=BC,$\widehat{CD}$=$\widehat{FD}$,
∴CD=FD,
在△BCD和△AFD中,
$\left\{\begin{array}{l}{BC=AF}\\{CD=FD}\\{DB=DA}\end{array}\right.$,
∴△BCD≌△AFD(SSS);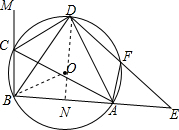 (3)连接DO并延长,交AB于点N,连接OB,
(3)连接DO并延长,交AB于点N,连接OB,
∵DB=DA,
∴$\widehat{DB}$=$\widehat{DA}$,
∴DN⊥AB,
∵∠ACM=120°,
∴∠ABD=∠ACD=60°,
∵DB=DA,
∴△ABD是等边三角形,
∴∠OBA=30°,
∴ON=$\frac{1}{2}$OB=$\frac{1}{2}$×5=2.5,
∴DN=ON+OD=7.5,
∴BD=$\frac{DN}{sin60°}$=5$\sqrt{3}$,
∴AD=BD=5$\sqrt{3}$,
∵$\widehat{BC}$=$\widehat{AF}$,
∴$\widehat{AC}$=$\widehat{BF}$,
∴∠ADC=∠BDF,
∵∠ABD=∠ACD,
∴△ACD∽△EBD,
∴$\frac{CD}{BD}=\frac{AD}{DE}$,
∴$\frac{6}{5\sqrt{3}}=\frac{5\sqrt{3}}{DE}$,
∴DE=12.5.
点评 此题属于圆的综合题,考查了圆周角定理、弧与弦的关系、等边三角形的判定与性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

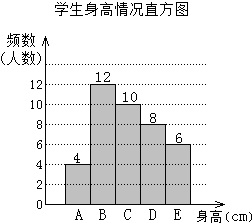 为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:
为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:(1)在样本中,学生的身高众数在B组,中位数在C组;
(2)若将学生身高情况绘制成扇形统计图,则C组部分的圆心角为90°;
(3)已知该校共有学生2000人,请估计身高在165及以上的学生约有多少人?
身高情况分组表(单位:cm)
| 组别 | 身高 |
| A | x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | x≥170 |
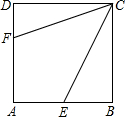 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3$\sqrt{5}$,且∠ECF=45°,则CF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3$\sqrt{5}$,且∠ECF=45°,则CF的长为( )| A. | 2$\sqrt{10}$ | B. | 3$\sqrt{5}$ | C. | $\frac{5}{3}\sqrt{10}$ | D. | $\frac{10}{3}\sqrt{5}$ |
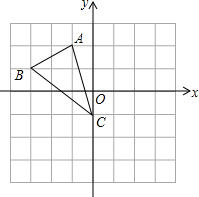 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上: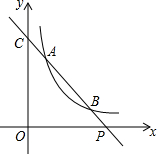 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
