题目内容
2. 如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数 y=$\frac{m}{x}$的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数 y=$\frac{m}{x}$的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.(1)求上述一次函数与反比例函数的表达式;
(2)设点Q是一次函数y=kx+3图象上的一点,且满足S△DOQ=2S△COD,求点Q的坐标.
分析 (1)令一次函数解析式中x=0,求出对应的y值,确定出D的坐标,得到OD的长,再由已知条件得到OB的长,由OD+OB求出BD的长,在直角三角形BDP中,利用两直角边乘积的一半表示出三角形的面积,将BD及已知的面积代入求出BP的长,确定出P的坐标,由P为一次函数与反比例函数的交点,将P的坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将P的坐标代入反比例函数解析式中求出m的值,确定出反比例函数解析式;
(2)先求得C的坐标,进而根据S△DOQ=2S△COD,求得MQ=2OC=4,然后分两种情况讨论求得.
解答 解:(1)∵一次函数y=kx+3的图象交y轴于点D,
∴OD=3.
∵B(0,-6),
∴BD=3+6=9,
∵S△DBP=27,
∴$\frac{1}{2}$•BD•BP=27,
∴BP=6,
∴P(6,-6);
把点P的坐标代入y=kx+3得:k=-$\frac{3}{2}$,
∴一次函数的解析式为:y=-$\frac{3}{2}$x+3,
把点P的坐标代入y=$\frac{m}{x}$得:m=-36.
∴反比例函数的表达式是y=-$\frac{36}{x}$;
(2)∵一次函数y=-$\frac{3}{2}$x+3的图象交x轴于点C,
∴把y=0代入求出x=2,即点C的坐标是(2,0),OC=2,
分为两种情况:当Q在射线DC上时,过Q作QM⊥y轴于M.
∵△DOQ的面积是△COD面积的2倍,
∴$\frac{1}{2}$OD•MQ=2×$\frac{1}{2}$OD•DC,
∴MQ=2OC=4,
把x=4代入y=-$\frac{3}{2}$x+3得:y=-3,即此时Q(4,-3),
当Q在射线CD上时,同法求出QM=4,
把x=-4代入y=-$\frac{3}{2}$x+3得:y=9,即此时Q(-4,9),
∴Q的坐标是(-4,9)或(4,-3).
点评 此题考查了一次函数与反比例函数的交点,以及利用待定系数法求函数解析式,其中利用待定系数法确定出两函数解析式是求两函数交点的关键.

| A. | 2x2÷x2=2x | B. | (-a2b)3=-6a6b3 | C. | 3x2+2x2=5x4 | D. | (x-3)2=x2-9 |
| A. | 众数 | B. | 平均数 | C. | 方差 | D. | 中位数 |
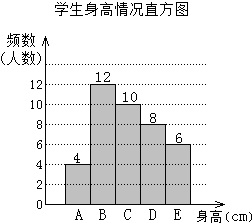 为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:
为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:(1)在样本中,学生的身高众数在B组,中位数在C组;
(2)若将学生身高情况绘制成扇形统计图,则C组部分的圆心角为90°;
(3)已知该校共有学生2000人,请估计身高在165及以上的学生约有多少人?
身高情况分组表(单位:cm)
| 组别 | 身高 |
| A | x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | x≥170 |
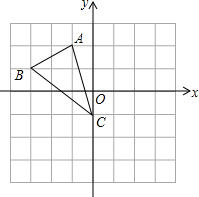 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上:
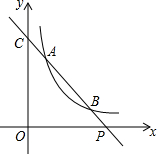 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.