题目内容
6.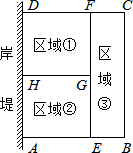 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
分析 (1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,并求出x的范围即可;
(2)利用二次函数的性质求出y的最大值,以及此时x的值即可.
解答 解:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=FC=a,则AE=HG=DF=2a,
∴DF+FC+HG+AE+EB+EF+BC=80,即8a+2x=80,
∴a=-$\frac{1}{4}$x+10,3a=-$\frac{3}{4}$x+30,
∴y=(-$\frac{3}{4}$x+30)x=-$\frac{3}{4}$x2+30x,
∵a=-$\frac{1}{4}$x+10>0,
∴x<40,
则y=-$\frac{3}{4}$x2+30x(0<x<40);
(2)∵y=-$\frac{3}{4}$x2+30x=-$\frac{3}{4}$(x-20)2+300(0<x<40),且二次项系数为-$\frac{3}{4}$<0,
∴当x=20时,y有最大值,最大值为300平方米.
点评 此题考查了二次函数的应用,以及列代数式,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
相关题目
14.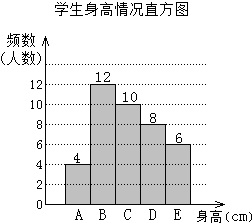 为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:
为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:
(1)在样本中,学生的身高众数在B组,中位数在C组;
(2)若将学生身高情况绘制成扇形统计图,则C组部分的圆心角为90°;
(3)已知该校共有学生2000人,请估计身高在165及以上的学生约有多少人?
身高情况分组表(单位:cm)
 为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:
为了解某校学生的身高情况,随机抽取该校若干名学生进行抽样调查.利用所得数据绘制如下统计图表:根据图表提供的信息,回答下列问题:(1)在样本中,学生的身高众数在B组,中位数在C组;
(2)若将学生身高情况绘制成扇形统计图,则C组部分的圆心角为90°;
(3)已知该校共有学生2000人,请估计身高在165及以上的学生约有多少人?
身高情况分组表(单位:cm)
| 组别 | 身高 |
| A | x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | x≥170 |
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |

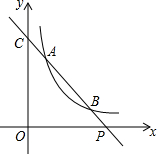 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.