题目内容
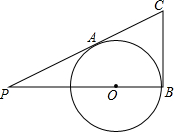 如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?
如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?考点:切线的性质
专题:
分析:如图,连接AO.根据切线的性质判定∠PAO=∠PBC=90°,则易证△PAO∽△PBC,由该相似三角形的对应边成比例进行解答.
解答: 解:如图,连接AO.
解:如图,连接AO.
∵PC、BC都是⊙O的切线,
∴∠PAO=∠PBC=90°,
又∵∠P=∠P,
∴△PAO∽△PBC,
∴
=
.
则
=
.
又∵CB:PC=1:2,OA=OB,
∴
=
=2.
 解:如图,连接AO.
解:如图,连接AO.∵PC、BC都是⊙O的切线,
∴∠PAO=∠PBC=90°,
又∵∠P=∠P,
∴△PAO∽△PBC,
∴
| OA |
| CB |
| PO |
| PC |
则
| PO |
| OA |
| PC |
| CB |
又∵CB:PC=1:2,OA=OB,
∴
| PO |
| OB |
| PC |
| CB |
点评:本题考查了切线的判定与性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2013年12月15日,“玉兔号”月球车月面软着陆后离地球380000千米,能够看到地球等离子层的全貌.380000千米用科学记数法表示为( )
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.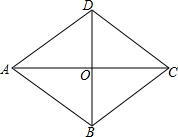 如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为
如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为 如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.
如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC. (1)先观察下列等式,再完成题后问题:
(1)先观察下列等式,再完成题后问题: