题目内容
 (1)先观察下列等式,再完成题后问题:
(1)先观察下列等式,再完成题后问题:| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
①请你猜想:
| 1 |
| 2010×2011 |
②若a、b为有理数,且|a-1|+(ab-2)2=0,求:
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2009)(b+2009) |
(2)如图,把一个面积为1的正方形等分成两个面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
考点:规律型:图形的变化类,有理数的混合运算
专题:
分析:(1)①根据题意类比得出
=
-
;
②先根据非负数的性质得出a、b的值,代入原式变形为1-
+
-
+
-
…+
-
是解题的关键;
(2)由数据和图象可知,利用正方形的面积减去最后的一个小长方形的面积来求解面积和即可.
| 1 |
| 2010×2011 |
| 1 |
| 2010 |
| 1 |
| 2011 |
②先根据非负数的性质得出a、b的值,代入原式变形为1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2011 |
(2)由数据和图象可知,利用正方形的面积减去最后的一个小长方形的面积来求解面积和即可.
解答:解:(1)①
=
-
;
②∵|a-1|+(ab-2)2=0,
∴a-1=0,ab-2=0,
∴a=1,b=2(2分)
原式=1-
+
-
+
-
…+
-
=1-
=
;
(2)
+
+
+
+
+
+
+
=1-
=
.
| 1 |
| 2010×2011 |
| 1 |
| 2010 |
| 1 |
| 2011 |
②∵|a-1|+(ab-2)2=0,
∴a-1=0,ab-2=0,
∴a=1,b=2(2分)
原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2011 |
=1-
| 1 |
| 2011 |
=
| 2010 |
| 2011 |
(2)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
=1-
| 1 |
| 256 |
=
| 255 |
| 256 |
点评:此题考查数字的变化规律和图形的变化规律,从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律,利用规律解决问题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
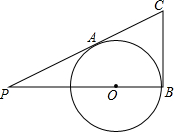 如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?
如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?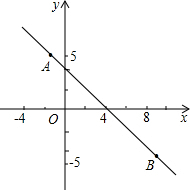 如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到,
如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到, 如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.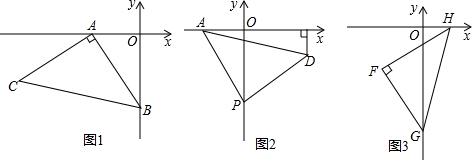
 已知AB=AC,∠BAC=90°,l经过点A,BD⊥l于D,CE⊥l于E,BD=6cm,CE=4cm,求S△ABC.
已知AB=AC,∠BAC=90°,l经过点A,BD⊥l于D,CE⊥l于E,BD=6cm,CE=4cm,求S△ABC.