题目内容
如图，AB、CD是⊙O的直径，弦DE∥AB，连接AE、AC．求证：AE=AC．考点：圆周角定理,圆心角、弧、弦的关系
专题：证明题
分析：连结OE，如图，根据平行线的性质由DE∥AB得到∠1=∠3，∠2=∠D，加上∠D=∠3，则∠1=∠2，根据圆心角、弧、弦的关系得到
=
，于是有AC=AE．
 |
| AC |
|
| AE |
解答：证明：
连结OE，如图，
∵DE∥AB，
∴∠1=∠3，∠2=∠D，
而OE=OD，
∴∠D=∠3，
∴∠1=∠2，
∴
=
，
∴AC=AE．
连结OE，如图，∵DE∥AB，
∴∠1=∠3，∠2=∠D，
而OE=OD，
∴∠D=∠3，
∴∠1=∠2，
∴
|
| AC |
|
| AE |
∴AC=AE．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了圆心角、弧、弦的关系．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
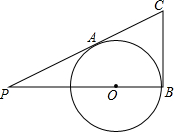如图，PC切⊙O于点A，PO的延长线交⊙O于点B，BC切⊙O于点B，若CB：PC=1：2，则PO：OB是多少？
如图，BD、CE是△ABC的高，△ADE与△ABC相似吗？为什么？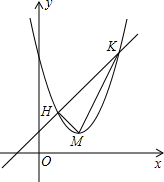
如图，抛物线y=x2-4x+5顶点为M，平移直线y=x交抛物线于点H、K，若S△MHK=3，求平移后直线的解析式．
如图，在△ABC中，AB=AC，D是AC上一点，过D作DE⊥BC于E，与BA的延长线交于F，求证：AD=AF．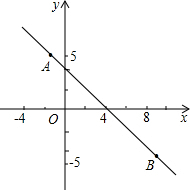
如图，已知直线y=kx+b过点（-1，5），且可由直线y=-x+2平移得到，
如图，在梯形ABCD中，AB∥CD，AD=BC，延长AB到E，使BE=DC．试判断AC与CE的大小关系？并说明理由．