题目内容
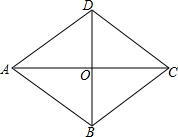 如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为
如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为考点:菱形的性质,切线的性质
专题:
分析:由题意可知该圆为菱形的内切圆,则其半径为O点到菱形边的距离,在Rt△AOB中可求得该距离,进一步可求得该圆的面积.
解答:解:由题意可知当圆为菱形的内切圆时面积最大,其半径r为O点到AB的距离,
∵四边形ABCD为菱形,
∴AO=
AC=4cm,BO=
BD=3cm,
在Rt△AOB中可求得AB=5,由面积相等可得AB•r=AO•BO,
即5r=3×4,解得r=2.4cm,
∴S圆=πr2=2.42×π=5.76πcm2,
故答案为:5.76π.
∵四边形ABCD为菱形,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOB中可求得AB=5,由面积相等可得AB•r=AO•BO,
即5r=3×4,解得r=2.4cm,
∴S圆=πr2=2.42×π=5.76πcm2,
故答案为:5.76π.
点评:本题主要考查菱形的性质,确定出最大面积的圆是菱形的内切圆是解题的关键.注意等积法的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图是一个几何体的三视图,则这个几何体的表面积为( )
如图是一个几何体的三视图,则这个几何体的表面积为( )| A、50π | B、100π |
| C、150π | D、175π |
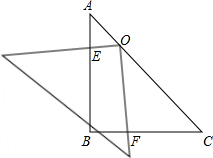 在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.
在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.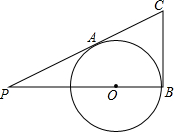 如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?
如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少? 如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么?
如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么? 如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.
如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.