题目内容
3.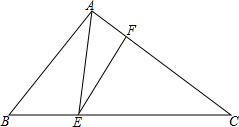 已知:如图,△ABC中,点E、F分别在BC和AC上,BE:BC=1:3,AF:AC=2:5,S△ABC=4,求S△AEF.
已知:如图,△ABC中,点E、F分别在BC和AC上,BE:BC=1:3,AF:AC=2:5,S△ABC=4,求S△AEF.
分析 根据BE:BC=1:3,得到S△AEC=$\frac{2}{3}$S△ABC=$\frac{2}{3}$×4=$\frac{8}{3}$,由于AF:AC=2:5,于是得到$\frac{{S}_{△AEF}}{{S}_{△AEC}}$=$\frac{2}{5}$,即可得到结论.
解答 解:∵ BE:BC=1:3,
BE:BC=1:3,
∴CE:BC=2:3,
∵S△ABC=4,
∴S△AEC=$\frac{2}{3}$S△ABC=$\frac{2}{3}$×4=$\frac{8}{3}$,
∵AF:AC=2:5,
∴$\frac{{S}_{△AEF}}{{S}_{△AEC}}$=$\frac{2}{5}$,
∴S△AEF=$\frac{2}{5}×$$\frac{8}{3}$=$\frac{16}{15}$.
点评 本题考查了三角形的面积,知道等高三角形的面积的比就等于三角形的底的比是解题的关键.

练习册系列答案
相关题目
8.下列各数中,最小的是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | -3 | D. | -1 |
15.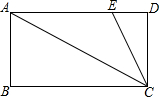 如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
 如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )| A. | 10 | B. | 15 | C. | 20 | D. | 40 |
 如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.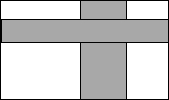 如图,要设计一幅长60cm、宽40cm的图案,其中有一横一竖的彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的$\frac{1}{2}$,求横彩条的宽度.
如图,要设计一幅长60cm、宽40cm的图案,其中有一横一竖的彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的$\frac{1}{2}$,求横彩条的宽度.