题目内容
17.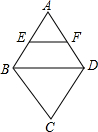 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是6.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是6.
分析 易证△ABD是等边三角形.再根据中位线定理易求BD.
解答 解:∵四边形ABCD是菱形,
∴AB=AD,
∵E、F分别是AB、AD的中点,
∴AE=AF,
又∵∠A=60°,
∴△AEF是等边三角形.
∴AB=AD=BD,
∵E、F分别是AB、AD的中点,
∴AB=2AE=2EF=2×3=6.
故答案为:6.
点评 本题考查了三角形中位线及菱形的性质,比较简单.如果三角形中位线的性质没有记住,还可以利用△AEF与△ABD的相似比为1:2,得出正确结论.

练习册系列答案
相关题目
7.如图,DE∥AB,则∠B的大小为( )

| A. | 42° | B. | 45° | C. | 48° | D. | 58° |
8.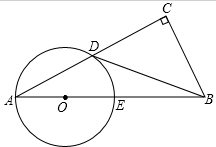 如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(I)求证:BD与⊙O相切.
(2)若点D是AC的中点.求tan∠DBA的值.
 如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.(I)求证:BD与⊙O相切.
(2)若点D是AC的中点.求tan∠DBA的值.
12.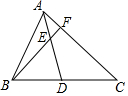 如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
 如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )
如图,AD是△ABC的中线,E是AD上一点,且AE:ED=1:2,BE的延长线交AC于F,则AF:FC=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
 如图,D、E分别在BC、AC上,AD、BE交于点F,且CD=2BD,CE=3AE,则BF:EF的值为2:1.
如图,D、E分别在BC、AC上,AD、BE交于点F,且CD=2BD,CE=3AE,则BF:EF的值为2:1.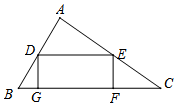 在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.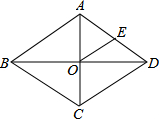 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5.
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5. 如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.
如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.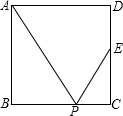 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )