题目内容
解方程：
①2（2x-1）2=8
②3（1-3x）3+24=0．
①2（2x-1）2=8
②3（1-3x）3+24=0．
考点：立方根,平方根
专题：
分析：①方程两边除以2，再开方，即可得出一元一次方程，求出方程的解即可；
②移项，方程两边都除以3，即可得出一元一次方程，求出方程的解即可．
②移项，方程两边都除以3，即可得出一元一次方程，求出方程的解即可．
解答：解：①方程两边除以2得：（2x-1）2=4，
开方得：2x-1=±2，
解得：x1=
，x2=-
；
②移项得：3（1-3x）3=-24，
（1-3x）3=-8，
1-3x=-2，
x=1．
开方得：2x-1=±2，
解得：x1=
| 3 |
| 2 |
| 1 |
| 2 |
②移项得：3（1-3x）3=-24，
（1-3x）3=-8，
1-3x=-2，
x=1．
点评：本题考查了立方根和平方根的应用，解此题的关键是能得出一元一次方程．
练习册系列答案
名校课堂系列答案
相关题目
半径为r的圆，内接正方形的边长与内接正三角形的边长的比为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在四边形ABCD中，AB=CD，AD=CB，求证：∠A=∠C．
如图，在Rt△ABC中，∠C=90°，∠1=∠2，若AB=15，CD=4，求△ABD的面积．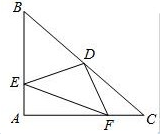
如图，△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，若BE=12，CF=5，求△DEF的面积．
在△ABC中，∠ACB=90°，S△BFC：S△AFC=1：3，BC=12，EF⊥BC于点E，求EB的长．