题目内容
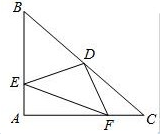 如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5,求△DEF的面积.
如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5,求△DEF的面积.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:首先连接AD,由△ABC是等腰直角三角形,AB=AC,AD是斜边的中线,可得:AD=DC,∠EAD=∠C=45°,AD⊥BC即∠CDF+∠ADF=90°,又DE⊥DF,可得:∠EDA+∠ADF=90°,故∠EDA=∠CDF,从而可证:△AED≌△CFD,所以可得:AE=CF,AF=BC,DE=DF,即△EDF为等腰直角三角形,在Rt△AEF中,运用勾股定理可将EF的值求出,进而可求出DE、DF的值,代入S△EDF=
DE2进行求解.
| 1 |
| 2 |
解答:解: 连接AD,
连接AD,
∵在Rt△ABC中,AB=AC,AD为BC边的中线,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA).
∴AE=CF=5,同理AF=BE=12.
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169.
∴EF=13,
∵DE=DF,
∴△DEF为等腰直角三角形,DE2+DF2=EF2=169,
∴DE=DF=
,
∴S△DEF=
×
×2=
.
 连接AD,
连接AD,∵在Rt△ABC中,AB=AC,AD为BC边的中线,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF
在△AED与△CFD中,
|
∴△AED≌△CFD(ASA).
∴AE=CF=5,同理AF=BE=12.
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169.
∴EF=13,
∵DE=DF,
∴△DEF为等腰直角三角形,DE2+DF2=EF2=169,
∴DE=DF=
13
| ||
| 2 |
∴S△DEF=
| 1 |
| 2 |
| 169 |
| 4 |
| 169 |
| 4 |
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
下列各数中,结果为负数的是( )
| A、-(-3) |
| B、-(-3)2 |
| C、(-3)2 |
| D、|-3| |
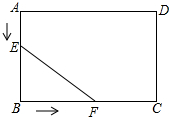 如图,在矩形ABCD中,AB=6cm,BC=8cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达C点时,两点同时停止运动,问经过几秒后△EBF的面积为5cm2?
如图,在矩形ABCD中,AB=6cm,BC=8cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达C点时,两点同时停止运动,问经过几秒后△EBF的面积为5cm2?