题目内容
20.若两个连续正数的平方和是313,求这两个连续正整数.分析 设出其中的一个正整数,然后表示出另一个正整数,利用平方和为313列出方程求解即可.
解答 解:设第一个正整数为x,则下一个正整数为(x+1),根据题意得:
x2+(x+1)2=313,
解得:x=-13(舍去),或x=12.
故另一个正整数为:x+1=12+1=13.
答:这两个连续正整数为12和13.
点评 本题考查了一元二次方程的应用,题目中的等量关系比较明显,难点是如何设出一个并表示出另一个未知数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在直角坐标系中,点P(-3,6)关于原点对称的点是( )
| A. | (-3,-6) | B. | (3,6) | C. | (3,-6) | D. | (6,-3) |
 如图,已知△ABC的边AB、BC上两点D、E,△ABE是关于DE的轴对称图形.四边形ADEC是关于直线AE的轴对称图形,求△ABC各内角的度数.
如图,已知△ABC的边AB、BC上两点D、E,△ABE是关于DE的轴对称图形.四边形ADEC是关于直线AE的轴对称图形,求△ABC各内角的度数.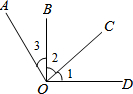 如图所示,已知∠AOC=∠BOD=90°,∠1=30°.
如图所示,已知∠AOC=∠BOD=90°,∠1=30°.