题目内容
7.阅读下列材料:1×2=$\frac{1}{3}$×(1×2×3-0×1×2),
2×3=$\frac{1}{3}$×(2×3×4-1×2×3),
3×4=$\frac{1}{3}$×(3×4×5-2×3×4),
由以上三个等式相加,可得 1×2+2×3+3×4=$\frac{1}{3}$(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4)=$\frac{1}{3}$×3×4×5=20.
读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程);
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2).
分析 由1×2=$\frac{1}{3}$(1×2×3-0×1×2),2×3=$\frac{1}{3}$(2×3×4-1×2×3),3×4=$\frac{1}{3}$(3×4×5-2×3×4),…,得出n(n+1)=$\frac{1}{3}$[(n(n+1)(n+2)-(n-1)n(n+1)],由此规律进一步拆开抵消得出答案即可.
解答 解:(1)1×2+2×3+3×4+…+10×11
=$\frac{1}{3}$(1×2×3-0×1×2+2×3×4-1×2×3+…+10×11×12-9×10×11)
=$\frac{1}{3}$×10×11×12
=440.
(2)1×2+2×3+3×4+…+n×(n+1)
=$\frac{1}{3}$[1×2×3-0×1×2+2×3×4-1×2×3+…+n(n+1)(n+2)-(n-1)n(n+1)]
=$\frac{1}{3}$n(n+1)(n+2).
点评 此题主要考查数字的变化规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
相关题目
12.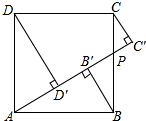 如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )
如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )
 如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )
如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )| A. | $\frac{4}{3}\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\frac{4}{3}$ |
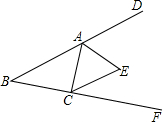 如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=69°.
如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=69°.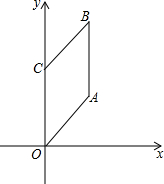 如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4).
如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4).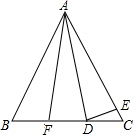 如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°. 如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.
如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.