题目内容
14．
如图C，D是线段AB上的两点，M，N分别是AC，BD的中点，若CD=6cm，MN=9cm，求线段AB的长．
分析 先利用线段中点的定义得到MC=$\frac{1}{2}$AC，DN=$\frac{1}{2}$BD，再利用MC+CD+DN=MN可得AC+BD=6，然后根据AB=AC+CD+BD进行计算即可．
解答 解：∵M、N分别是线段AC，BD的中点，
∴MC=$\frac{1}{2}$AC，DN=$\frac{1}{2}$BD，
∵MC+CD+DN=MN=9cm，
∴MC+DN=9-6=3cm
∴AC+BD=2MC+2DN=2×3=6，
∴AB=AC+CD+BD=AC+BD+CD=6+6=12（cm），
即线段AB的长为12cm．
点评 本题考查了两点间的距离的求法，解题时利用了线段的和差，线段中点的性质，解决此类问题的关键是找出各个线段间的关系．
练习册系列答案
阅读快车系列答案
相关题目
18．两个相似多边形的一组对应边分别是3cm和4.5cm，如果它们的面积之和是78cm2，那么较大的多边形的面积是（ ）
| A． | 44.8 | B． | 42 | C． | 52 | D． | 54 |
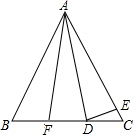如图，△ABC中，∠B=∠C，AB=AC，D、F在BC边上，BF=CD，E在AC边上，∠ADE=∠AED，∠EDC=23°，则∠FAC=46°．
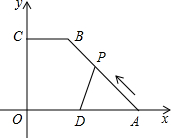已知，如图，在直角梯形COAB中，CB∥OA，以O为原点建立平面直角坐标系，A、B、C的坐标分别为A（10，0）、B（4，8）、C（0，8），D为OA的中点，动点P自A点出发沿A→B→C→O的路线移动，速度为每秒1个单位，移动时间记为t秒，
如图，在△ABC中，AB=AC，∠A=40°，BD是∠ABC的平分线，求∠BDC的度数．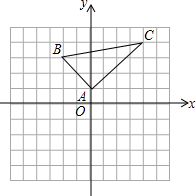
如图，在平面直角坐标系中，A（0，1），B（-2，3），C（4，4）．