题目内容
7.在图1直角坐标系中,矩形OABC的点A、C分别在x轴和y轴的正半轴上,B点在第一象限(1)若矩形OABC的面积为16$\sqrt{3}$,且OA=$\sqrt{3}$AB,求点B的坐标;
(2)D点是x轴负半轴上的一点,且AC=AD,连CD,M是CD的中点,求证:OM⊥BM;
(3)在(1)的条件下,P为BC边上的一点,且∠COP=30°,OQ平分∠BOP,E、F是OB、OQ上的动点,求BF+EF的最小值,请在图2中画出示意图并简述理由.
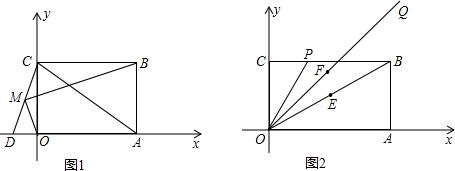
分析 (1)由矩形的面积和边长之间的关系求出AB、OA即可得出结果;
(2)连接OB交AC于N,先证明MN是△ADC的中位线,得出MN=$\frac{1}{2}$AD,再由AD=AC=BO,得出MN=$\frac{1}{2}$BO,根据直角三角形的判定方法即可得出结论;
(3)作BH⊥OP于H,交OQ于F,作FE⊥OB于E,E、F即为使BF+EF得最小值的点,再根据角平分线的性质即可得出结果.
解答 解:(1)∵矩形OABC的面积为16$\sqrt{3}$,且OA=$\sqrt{3}$AB,
∴$\sqrt{3}$AB2=16$\sqrt{3}$,
∴AB=4,
∴OA=4$\sqrt{3}$,
∴点B的坐标为(4$\sqrt{3}$,4);
(2)连接OB交AC于N,如图1所示: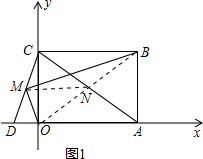 ∵M是CD的中点,
∵M是CD的中点,
∴CM=DM,
∵四边形OABC是矩形,
∴AN=CN,BN=ON,AC=BO,
∴MN是△ADC的中位线,
∴MN=$\frac{1}{2}$AD,
∵AD=AC,
∴AD=BO,
∴MN=$\frac{1}{2}$BO,
∴∠OMB=90°,
∴OM⊥BM;
(3)作BH⊥OP于H,交OQ于F,作FE⊥OB于E,E、F即为使BF+EF得最小值的点;如图2所示: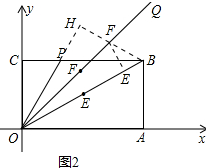
∵tan∠AOB=$\frac{AB}{OA}=\frac{4}{4\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠AOB=30°,
∴∠BOH=90°-∠COP-∠AOB=30°,
∴∠BOH=∠AOB,
∴BH=AB=4,
∵OQ平分∠BOP,
∴HF=EF,
∴BF+EF=BF+HF=BH=4,
即BF+EF的最小值为4.
点评 本题是四边形综合题,考查了矩形的性质、三角形中位线定理、直角三角形的判定方法、锐角三角函数以及最小值问题等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线才能得出答案.

| A. | 44.8 | B. | 42 | C. | 52 | D. | 54 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
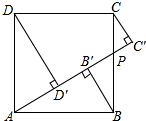 如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )
如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )| A. | $\frac{4}{3}\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\frac{4}{3}$ |
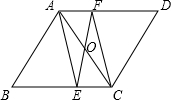 在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.
在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.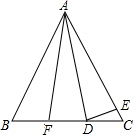 如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.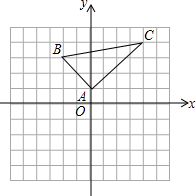 如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).
如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).