题目内容
11．
如图，由两个等宽的矩形叠合而得到的四边形ABCD是菱形吗？证明你的结论．
分析 作AR⊥BC于R，AS⊥CD于S，根据题意先证出四边形ABCD是平行四边形，再由BC=CD得平行四边形ABCD是菱形．
解答 四边形ABCD是菱形．
证明：如图，
作AR⊥BC于R，AS⊥CD于S，
由题意知：AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵矩形BEDG和矩形BNDQ中，BE=BN，DE=DN，
∴两个矩形全等，
∴AR=AS，
∵AR•BC=AS•CD，
∴BC=CD，
∴平行四边形ABCD是菱形．
点评 此题主要考查了菱形的判定，熟练掌握矩形的性质，菱形的判定方法是解题关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
1．顺次连接对角线相等的四边形的各边中点，所得图形一定是（ ）
| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 正方形 |
2．若3×27m÷9m=36，则正整数m的值是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
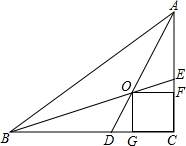如图，在Rt△ABC中，两锐角的平分线AD，BE相交于点O，OF⊥AC于点F，OG⊥BC于点G，求证：四边形OGCF是正方形．
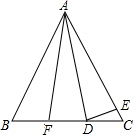如图，△ABC中，∠B=∠C，AB=AC，D、F在BC边上，BF=CD，E在AC边上，∠ADE=∠AED，∠EDC=23°，则∠FAC=46°．
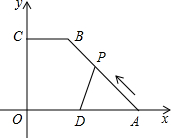已知，如图，在直角梯形COAB中，CB∥OA，以O为原点建立平面直角坐标系，A、B、C的坐标分别为A（10，0）、B（4，8）、C（0，8），D为OA的中点，动点P自A点出发沿A→B→C→O的路线移动，速度为每秒1个单位，移动时间记为t秒，