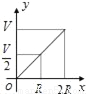
��Ŀ����
�Ķ���������ʽx2+2x+3ת��Ϊ��x+m��2+k����ʽ������m��kΪ����������x2+2x+3=x2+2x+1��1+3=��x+1��2+2������m=1��k=2��
��1�����մ˷�������ʽx2+6x+15��Ϊ��x+m��2+k����ʽ����ָ��m��k��ֵ��
��2��������ʽx2��6x+a�ɻ�Ϊ��x��b��2��1����ʽ����b��a��ֵ��
��1��x2+6x+15=��x+3��2+6��m=3��k=6����2��b��a=��5�� ����������������� ��1��������ʽ�䷽���ɣ� ��2���Ƚ�����ʽ�䷽�������䷽���ʽ�Ӻʹ���ʽ�Աȼ��ɵõ���ֵ���ٴ����м��㼴��. ��������� ��1���� x2+6x+15=x2+6x+32+6=��x+3��2+6�� ��m=3��k=6�� ��2����x2��6x+a=x2��6x+9��9+a...
��ϰ��ϵ�д�
�����Ŀ
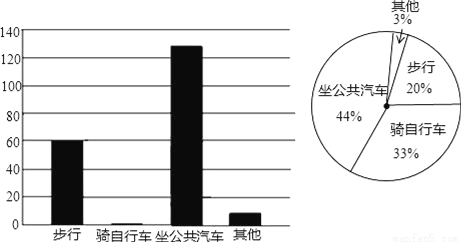
ij��ѧ����Ǩ��У�ᣬ��Ǩ����У��֮ǰ��ͬѧ�Ǿ�Уѧ����ε�У���������һ�ε��飬�����������Ƴ��˱�������ͼ������ͳ��ͼ���������ͼ����Ϣ������и��⣺
��1���˴ι������˶���λѧ����
��2���뽫�������������
���� | �����г� | ���������� | ���� |
60 |
��3���뽫����ͳ��ͼ����������


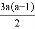 ��ֵ��_____��
��ֵ��_____��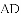
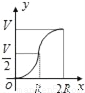 B.
B. 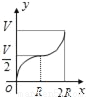 C.
C.  D.
D.