题目内容
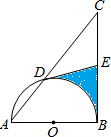 如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-6x+8=0的两个根,则图中阴影部分的面积为
如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-6x+8=0的两个根,则图中阴影部分的面积为考点:扇形面积的计算,解一元二次方程-因式分解法,切线的判定与性质
专题:计算题
分析:先利用因式分解法解方程求出AD、AB的长,然后连接OD、BD、OE,并判定△AOD是等边三角形,根据直径所对的圆周角是直角可得BD⊥AC,根据直角三角形斜边上的中线等于斜边的一半可得DE=
BC=BE,再根据到线段两端点距离相等的点在线段的垂直平分线上可得OE垂直平分BD,然后根据勾股定理求出BD的长,再根据相似三角形对应边成比例列式求出BC的长,从而得到BE的长度,最后根据阴影部分的面积等于四边形OBED的面积减去扇形BOD的面积,列式进行计算即可求解.
| 1 |
| 2 |
解答: 解:x2-6x+8=0,
解:x2-6x+8=0,
(x-2)(x-4)=0,
∴x-2=0,x-4=0,
解得x1=2,x2=4,
∴AD=2,AB=4,
∵AB是直径,
∴AO=BO=
AB=2,
连接OD,则AO=OD=AD=2,
∴△AOD是等边三角形,
连接BD,则BD⊥AC,
∵E是BC边的中点,
∴DE=BE=
BC,
连接OE,则OE是线段BD的垂直平分线,
在Rt△AOD中,BD=
=
=2
,
∵∠A=∠A,∠ADB=∠ABC=90°,
∴△ABC∽△ADB,
∴
=
,
即
=
,
解得BC=4
,
BE=
BC=2
,
∴S四边形OBED=2S△OBE=2×
×2×2
=4
,
又∠BOD=180°-∠AOD=180°-60°=120°,
∴S扇形BOD=
=
π,
∴阴影部分的面积=S四边形OBED-S扇形BOD=4
-
π.
故答案为:4
-
π.
 解:x2-6x+8=0,
解:x2-6x+8=0,(x-2)(x-4)=0,
∴x-2=0,x-4=0,
解得x1=2,x2=4,
∴AD=2,AB=4,
∵AB是直径,
∴AO=BO=
| 1 |
| 2 |
连接OD,则AO=OD=AD=2,
∴△AOD是等边三角形,
连接BD,则BD⊥AC,
∵E是BC边的中点,
∴DE=BE=
| 1 |
| 2 |
连接OE,则OE是线段BD的垂直平分线,
在Rt△AOD中,BD=
| AB2+AD2 |
| 42-22 |
| 3 |
∵∠A=∠A,∠ADB=∠ABC=90°,
∴△ABC∽△ADB,
∴
| BC |
| BD |
| AB |
| AD |
即
| BC | ||
2
|
| 4 |
| 2 |
解得BC=4
| 3 |
BE=
| 1 |
| 2 |
| 3 |
∴S四边形OBED=2S△OBE=2×
| 1 |
| 2 |
| 3 |
| 3 |
又∠BOD=180°-∠AOD=180°-60°=120°,
∴S扇形BOD=
| 120°•π•22 |
| 360° |
| 4 |
| 3 |
∴阴影部分的面积=S四边形OBED-S扇形BOD=4
| 3 |
| 4 |
| 3 |
故答案为:4
| 3 |
| 4 |
| 3 |
点评:本题主要考查了扇形的面积计算,一元二次方程的求解,切线的性质,勾股定理,相似三角形的判定与性质,根据方程的解判断出△AOD是等边三角形是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 由于矩形和菱形特殊的对称美和矩形的四个角都是直角,从而为密铺提供了方便,因此墙砖一般设计为矩形,而且图案以菱形居多,如图3所示,是长为30cm,宽为20cm的一块矩形瓷砖,E、F、G、H分别是矩形四边的中点,阴影部分为黄色,其它部分为淡蓝色,现有一面长为6m,高为3m的墙面准备贴这种瓷砖,那么:这面墙要贴的瓷砖数及全部贴满后这面墙上最多出现的与图3中面积相等的菱形个数分别为( )
由于矩形和菱形特殊的对称美和矩形的四个角都是直角,从而为密铺提供了方便,因此墙砖一般设计为矩形,而且图案以菱形居多,如图3所示,是长为30cm,宽为20cm的一块矩形瓷砖,E、F、G、H分别是矩形四边的中点,阴影部分为黄色,其它部分为淡蓝色,现有一面长为6m,高为3m的墙面准备贴这种瓷砖,那么:这面墙要贴的瓷砖数及全部贴满后这面墙上最多出现的与图3中面积相等的菱形个数分别为( )| A、288、561 |
| B、300、561 |
| C、288、566 |
| D、300、566 |
设a=
-
,那么a是( )
| 3 | 12
| ||||||
| 3 | 7 |
| A、无理数 | B、正整数 |
| C、分数 | D、负整数 |

 某厂承印新课程标准实验教材,新书出厂时,要将打包成长、宽、高分别为x分米、y分米、z分米的长方体包装加上扎带(如图所示双虚线位置).若扎带每个接头处要多余0.5分米,则一个长方体包装上的扎带总长
某厂承印新课程标准实验教材,新书出厂时,要将打包成长、宽、高分别为x分米、y分米、z分米的长方体包装加上扎带(如图所示双虚线位置).若扎带每个接头处要多余0.5分米,则一个长方体包装上的扎带总长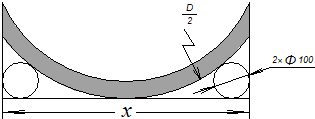 两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm. △ABC在直角坐标系中如图摆放,其中顶点A,B,C的坐标分别为(-4,1),(-1,-1),(-3,2),若将△ABC绕点B顺时针方向旋转90°,则A点的对应点的坐标为
△ABC在直角坐标系中如图摆放,其中顶点A,B,C的坐标分别为(-4,1),(-1,-1),(-3,2),若将△ABC绕点B顺时针方向旋转90°,则A点的对应点的坐标为