��Ŀ����
15�� ��M�ص�N����һ����ͨ��·����·��Ϊ120km����һ�����ٹ�·����·��Ϊ126km���׳����ҳ�ͬʱ��M�ؿ���N�أ��׳�ȫ������ͨ��·���ҳ�����ʻ����һ����ͨ��·��Ȼ�����ϸ��ٹ�·��������������ͨ��·���ٹ�·�Ϸֱ𱣳�������ʻ����������ͨ��·�ϵ��г��ٶ�Ϊ60km/h���ڸ��ٹ�·�ϵ��г��ٶ�Ϊ100km/h������������x hʱ����N�ص�·��Ϊy km��ͼ�е��߶�AB������ACD�ֱ��ʾ�׳����ҳ���y��x֮��ĺ�����ϵ��
��M�ص�N����һ����ͨ��·����·��Ϊ120km����һ�����ٹ�·����·��Ϊ126km���׳����ҳ�ͬʱ��M�ؿ���N�أ��׳�ȫ������ͨ��·���ҳ�����ʻ����һ����ͨ��·��Ȼ�����ϸ��ٹ�·��������������ͨ��·���ٹ�·�Ϸֱ𱣳�������ʻ����������ͨ��·�ϵ��г��ٶ�Ϊ60km/h���ڸ��ٹ�·�ϵ��г��ٶ�Ϊ100km/h������������x hʱ����N�ص�·��Ϊy km��ͼ�е��߶�AB������ACD�ֱ��ʾ�׳����ҳ���y��x֮��ĺ�����ϵ����1����գ�a=1.36��b=2��
��2�����߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3�������ں�ʱ�������N�ص�·��֮��ﵽ��30km��
���� ��1�����C���꣬�ٸ���ʱ��=$\frac{·��}{�ٶ�}$�ֱ�����׳�����ͨ��·����ʻ��ʱ�估�ҳ��ڸ��ٹ�·����ʻ��ʱ�䣬�ɵ�a��b��ֵ��
��2������A��B��C��D�ĵ��������ϵ�������ɵ��߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3���������ۣ���0��x��0.1ʱ���ɽ���ʽ��֪�ס���������������Ϊ12����0.1��x��1.36ʱ����y1-y2��30�в���ʽ�ɵ�x�ķ�Χ����1.36��x��2ʱ����y1��30�в���ʽ�ɵô�ʱx�ķ�Χ���ۺ�������������ɵô𰸣�
��� �⣺��1���������⣬֪����C������Ϊ��0.1��126����
��a=0.1+$\frac{126}{100}$=1.36��b=$\frac{120}{60}$=2��
�ʴ�Ϊ��1.36��2��
��2�����߶�AB����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy1=k1x+b1��
��A��0��120����B��2��0�����������ã�
$\left\{\begin{array}{l}{{b}_{1}=120}\\{2{k}_{1}+{b}_{1}=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{k}_{1}=-60}\\{{b}_{1}=120}\end{array}\right.$��
��y1=-60x+120��
���߶�CD����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy2=k2x+b2��
��C��0.1��126����D��1.36��0�����������ã�
$\left\{\begin{array}{l}{0.1{k}_{2}+{b}_{2}=126}\\{1.36{k}_{2}+{b}_{2}=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{k}_{2}=-100}\\{{b}_{2}=136}\end{array}\right.$��
��y2=-100x+136��
��3�������⣬�ٵ�x=0.1ʱ��������N�ص�·��֮����12km��
�൱0��x��0.1ʱ��������N�ص�·��֮����ܴﵽ��30km��
�ڵ�0.1��x��1.36ʱ����y1-y2��30���ã�-60x+120��-��-100x+136����30��
���x��1.15��
����1.15��x��1.36ʱ��������N�ص�·��֮��ﵽ��30km��
�۵�1.36��x��2ʱ����y1��30����-60x+120��30�����x��1.5��
����1.36��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
���ϣ���1.15��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
���� ������Ҫ����һ�κ�����ͼ����ϵ������������ʽ��һ�κ�����ʵ��Ӧ����������������ȷ�ķ��������ǽ���Ĺؼ���

 ��ͼ����֪�ı���ABCD�Ǿ��Σ��Խ���AC��BD���ڵ�P�������н�����ȷ���ǣ�������
��ͼ����֪�ı���ABCD�Ǿ��Σ��Խ���AC��BD���ڵ�P�������н�����ȷ���ǣ�������| A�� | AC�ǡ�BAD��ƽ���� | B�� | AC��BD | ||
| C�� | AC=BD | D�� | AC��2BP |

| A�� | 2 �� | B�� | 3�� | C�� | 4�� | D�� | 5�� |

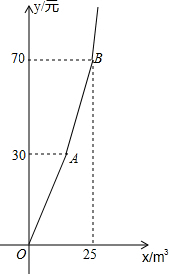 Ϊ��ǿ��·�Ľ�ˮ��ʶ����������ˮ��Դ��ij�жԾ�����ˮʵ�н���ˮ�ۣ������ͥÿ����ˮ������Ϊ�������ݣ�һ����������ˮ�ĵ���֮�ȵ���1��2����ͼ���߱�ʾʵ�н���ˮ�ۺ�ÿ��ˮ��y��Ԫ������ˮ��x��m3��֮��ĺ�����ϵ����������AB��ʾ�ڶ�������ʱy��x֮��ĺ�����ϵ��
Ϊ��ǿ��·�Ľ�ˮ��ʶ����������ˮ��Դ��ij�жԾ�����ˮʵ�н���ˮ�ۣ������ͥÿ����ˮ������Ϊ�������ݣ�һ����������ˮ�ĵ���֮�ȵ���1��2����ͼ���߱�ʾʵ�н���ˮ�ۺ�ÿ��ˮ��y��Ԫ������ˮ��x��m3��֮��ĺ�����ϵ����������AB��ʾ�ڶ�������ʱy��x֮��ĺ�����ϵ��