题目内容
在△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.探究:∠DAE与∠ABC,∠C的数量关系.
考点:三角形内角和定理
专题:
分析:作出图形,分①AB>AC时,根据直角三角形两锐角互余表示出∠BAD,再根据角平分线的定义和三角形内角和定理表示出∠BAE,然后根据∠DAE=∠BAD-∠BAE整理即可得解;②AB<AC时,同理可求.
解答: 解:如图,AB>AC时,∵AD⊥BC,
解:如图,AB>AC时,∵AD⊥BC,
∴∠BAD=90°-∠ABC,
∵AE平分∠BAC,
∴∠BAE=
(180°-∠ABC-∠C),
∴∠DAE=∠BAD-∠BAE=(90°-∠ABC)-
(180°-∠ABC-∠C)=
(∠C-∠ABC),
即∠DAE=
(∠C-∠ABC),
同理,AB<AC时,∠DAE=
(∠ABC-∠C).
 解:如图,AB>AC时,∵AD⊥BC,
解:如图,AB>AC时,∵AD⊥BC,∴∠BAD=90°-∠ABC,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
∴∠DAE=∠BAD-∠BAE=(90°-∠ABC)-
| 1 |
| 2 |
| 1 |
| 2 |
即∠DAE=
| 1 |
| 2 |
同理,AB<AC时,∠DAE=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余,要注意分情况讨论.整体思想的利用是解题的关键,作出图形更形象直观.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列各组二次根式中是同类二次根式的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
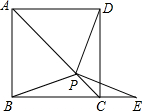 如图,在正方形ABCD中,P是对角线AC上的一动点(包括点A、点C),点E在直线BC上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一动点(包括点A、点C),点E在直线BC上,且PE=PB.
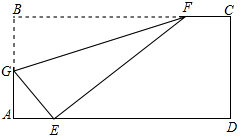 如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.
如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10. 如图,在△ABC中,AB=AC,D、E分别是AC,AB上的点,且BD=BC,BE=ED=AD,求∠A的度数.
如图,在△ABC中,AB=AC,D、E分别是AC,AB上的点,且BD=BC,BE=ED=AD,求∠A的度数.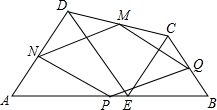 如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,
如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N, 已知点A、B在反比例函数y=
已知点A、B在反比例函数y=