题目内容
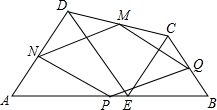 如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,
如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,(1)试判断四边形PQMN为怎样四边形,并证明你的结论.
(2)求∠NMQ的大小.
考点:中点四边形
专题:
分析:(1)连接四边形ADCB的对角线,通过全等三角形来证得AC=BD,从而根据三角形中位线定理证得四边形NPQM的四边相等,可得出四边形MNPQ是菱形.
(2)利用(1)中全等三角形的对应角相等得到∠ACE=∠DBE,由等边三角形的性质和三角形外角定理求得∴∠CEB=∠CAB+∠DBE=∠CAB+∠ACE=60°,则∠AOB=∠NMQ=120°.
(2)利用(1)中全等三角形的对应角相等得到∠ACE=∠DBE,由等边三角形的性质和三角形外角定理求得∴∠CEB=∠CAB+∠DBE=∠CAB+∠ACE=60°,则∠AOB=∠NMQ=120°.
解答: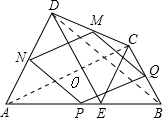 (1)解:四边形PQMN为菱形.理由如下:
(1)解:四边形PQMN为菱形.理由如下:
如图,连接BD、AC.
∵△ADE、△ECB是等边三角形,
∴AE=DE,EC=BE,∠AED=∠BEC=60°,
∴∠AEC=∠DEB=120°,
在△AEC与△DEB中,
,
∴△AEC≌△DEB(SAS),
∴AC=BD;
∵M、N是CD、AD的中点,
∴MN是△ACD的中位线,即MN=
AC;
同理可证得:NP=
DB,QP=
AC,MQ=
BD;
∴MN=NP=PQ=MQ,
∴四边形NPQM是菱形;
(2)∵由(1)知,△AEC≌△DEB,
∴∠ACE=∠DBE,
∴∠CEB=∠CAB+∠DBE=∠CAB+∠ACE=60°,
∴∠AOB=120°
又∵∠NMQ=∠DOC=∠AOB,
∴∠NMQ=120°.
 (1)解:四边形PQMN为菱形.理由如下:
(1)解:四边形PQMN为菱形.理由如下:如图,连接BD、AC.
∵△ADE、△ECB是等边三角形,
∴AE=DE,EC=BE,∠AED=∠BEC=60°,
∴∠AEC=∠DEB=120°,
在△AEC与△DEB中,
|
∴△AEC≌△DEB(SAS),
∴AC=BD;
∵M、N是CD、AD的中点,
∴MN是△ACD的中位线,即MN=
| 1 |
| 2 |
同理可证得:NP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=NP=PQ=MQ,
∴四边形NPQM是菱形;
(2)∵由(1)知,△AEC≌△DEB,
∴∠ACE=∠DBE,
∴∠CEB=∠CAB+∠DBE=∠CAB+∠ACE=60°,
∴∠AOB=120°
又∵∠NMQ=∠DOC=∠AOB,
∴∠NMQ=120°.
点评:此题主要考查的是菱形的判定方法,能发现并构建出全等三角形,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知(a+b)2=9,(a-b)2=4,则ab的值为( )
| A、13 | ||
| B、5 | ||
C、
| ||
D、
|
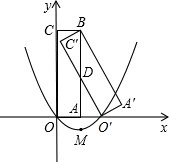 如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形.
如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形. 解不等式组
解不等式组 如图,一张边长为4的等边三角形纸片ABC,点E、F分别在AB、AC上,以EF为折痕对折纸片,使点A落在BC边上的点D处,则CF的最大值为
如图,一张边长为4的等边三角形纸片ABC,点E、F分别在AB、AC上,以EF为折痕对折纸片,使点A落在BC边上的点D处,则CF的最大值为