题目内容
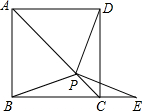 如图,在正方形ABCD中,P是对角线AC上的一动点(包括点A、点C),点E在直线BC上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一动点(包括点A、点C),点E在直线BC上,且PE=PB.(1)求证:△BCP≌△DCP;
(2)连接DE,求证:△DPE为等腰直角三角形;
(3)若AB=2
| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得BC=CD,∠ACB=∠ACD=45°,然后利用“边角边”证明△BCP和△DCP全等即可;
(2)根据全等三角形对应角相等可得∠CDP=∠CBP,根据等边对等角可得∠CBP=∠E,从而得到∠CDP=∠E,再根据三角形的内角和定理可得∠DPE=∠DCE=90°,然后根据等腰直角三角形的定义证明即可;
(3)根据等腰直角三角形的性质列式表示出△DPE面积,然后判断出点P与点A或C重合时,面积最大,点P与正方形的中心重合是面积最小,然后求解即可.
(2)根据全等三角形对应角相等可得∠CDP=∠CBP,根据等边对等角可得∠CBP=∠E,从而得到∠CDP=∠E,再根据三角形的内角和定理可得∠DPE=∠DCE=90°,然后根据等腰直角三角形的定义证明即可;
(3)根据等腰直角三角形的性质列式表示出△DPE面积,然后判断出点P与点A或C重合时,面积最大,点P与正方形的中心重合是面积最小,然后求解即可.
解答:(1)证明:在正方形ABCD中,BC=CD,∠ACB=∠ACD=45°,
在△BCP和△DCP中,
,
∴△BCP≌△DCP(SAS);
(2)证明:∵△BCP≌△DCP,
∴∠CDP=∠CBP,
∵PE=PB,
∴∠CBP=∠E,
∴∠CDP=∠E,
∴∠DPE=∠DCE=90°,
∴△DPE为等腰直角三角形;
(3)解:∵△DPE为等腰直角三角形,
∴△DPE面积=
DP2,
∴点P与点A或C重合时,面积最大,点P与正方形的中心重合是面积最小,
∵AB=2
,
∴△DPE面积的最大值=
×(2
)2=4,
最小值=
×(
×2
)2=2.
在△BCP和△DCP中,
|
∴△BCP≌△DCP(SAS);
(2)证明:∵△BCP≌△DCP,

∴∠CDP=∠CBP,
∵PE=PB,
∴∠CBP=∠E,
∴∠CDP=∠E,
∴∠DPE=∠DCE=90°,
∴△DPE为等腰直角三角形;
(3)解:∵△DPE为等腰直角三角形,
∴△DPE面积=
| 1 |
| 2 |
∴点P与点A或C重合时,面积最大,点P与正方形的中心重合是面积最小,
∵AB=2
| 2 |
∴△DPE面积的最大值=
| 1 |
| 2 |
| 2 |
最小值=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等边对等角的性质,等腰直角三角形的判断与性质,难点在于(3)判断出△DPE的面积最大和最小时点P的位置.

练习册系列答案
相关题目
已知(a+b)2=9,(a-b)2=4,则ab的值为( )
| A、13 | ||
| B、5 | ||
C、
| ||
D、
|
 如图,一张边长为4的等边三角形纸片ABC,点E、F分别在AB、AC上,以EF为折痕对折纸片,使点A落在BC边上的点D处,则CF的最大值为
如图,一张边长为4的等边三角形纸片ABC,点E、F分别在AB、AC上,以EF为折痕对折纸片,使点A落在BC边上的点D处,则CF的最大值为