题目内容
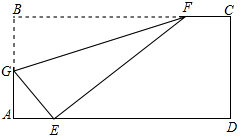 如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.
如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.(1)当BF的最小值等于多少时,才能使B点落在AD上一点E处;
(2)当F点与C点重合时,求AE的长;
(3)当AE=3时,点F离点B有多远?
考点:翻折变换(折叠问题)
专题:
分析:(1)当FE⊥AD时,BF的值最小,即可求出BF的最小值等于6.
(2)在RT△CDE中运用勾股定理求出DE,再利用AE=AD-DE即可求出答案.
(3)作FH⊥AD于点H,设AG=x,利用勾股定理可先求出AG,可得EG,利用△AEG∽△HFE,由
=
可求出EF,即得出BF的值.
(2)在RT△CDE中运用勾股定理求出DE,再利用AE=AD-DE即可求出答案.
(3)作FH⊥AD于点H,设AG=x,利用勾股定理可先求出AG,可得EG,利用△AEG∽△HFE,由
| EF |
| EG |
| FH |
| AE |
解答:解:(1)当FE⊥AD时,BF的值最小,
即BF=AB=6.当BF的最小值等于6时,才能使B点落在AD上一点E处;
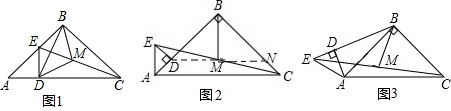
(2)如图1,

∵在RT△CDE中,CE=BC=10,CD=6,
∴DE=
=
=8,
∴AE=AD-DE=10-8=2,
(3)如图2,作FH⊥AD于点H,

AE=3,设AG=x,则BG=EG=6-x,
根据勾股定理得:
(6-x)2=x2+9,
x=
,
∴EG=BG=
,
又△AEG∽△HFE,
∴
=
,
=
,
∴EF=
,
∴BF=EF=
.
即BF=AB=6.当BF的最小值等于6时,才能使B点落在AD上一点E处;
(2)如图1,

∵在RT△CDE中,CE=BC=10,CD=6,
∴DE=
| CE2-CD2 |
| 102-62 |
∴AE=AD-DE=10-8=2,
(3)如图2,作FH⊥AD于点H,

AE=3,设AG=x,则BG=EG=6-x,
根据勾股定理得:
(6-x)2=x2+9,
x=
| 9 |
| 4 |
∴EG=BG=
| 15 |
| 4 |
又△AEG∽△HFE,
∴
| EF |
| EG |
| FH |
| AE |
| EF | ||
|
| 6 |
| 3 |
∴EF=
| 15 |
| 2 |
∴BF=EF=
| 15 |
| 2 |
点评:本题主要考查了翻折变换,解题的关键是折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
若把分式
中的x、y都扩大3倍,则分式的值( )
| x+3y |
| 2x-y |
| A、扩大3倍 | B、扩大9倍 |
| C、不变 | D、缩小到原来的 |
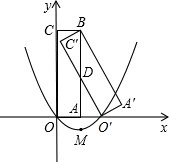 如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形.
如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形. 解不等式组
解不等式组