题目内容
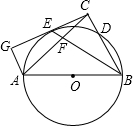 如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.
如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.(1)求证:CG为⊙O的切线;
(2)若AB=10,CG=8,求
| EF |
| BF |
考点:切线的判定
专题:
分析:(1)如图,连接OE,证明OE⊥CG即可解决问题;
(2)如图,连接AD;利用有关定理首先求出
的值,再求出
的值,进而求出线段EF、FB之间的数量关系问题即可解决.
(2)如图,连接AD;利用有关定理首先求出
| EF |
| FH |
| BH |
| BE |
解答: 解:(1)如图1,连接OE;
解:(1)如图1,连接OE;
∵BE平分∠ABC,
∴∠OBE=∠CBE;而OB=OE,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE;
∵CG⊥BC,
∴∠CEB+∠CBE=90°,
∴∠CEB+∠OEB=90°,
即OE⊥CG,
∴CG为⊙O的切线.
(2)如图2,连接AD,交BE于点H;
∵CG⊥BC,AG∥BC,
∴∠GCB=90°;
又∵AB为⊙O的直径,
∴∠ADB=90°,
∴四边形ADCG为矩形,
∴AD=GC=8,
由勾股定理得:
BD2=AB2-AD2=100-64=36,
∴BD=6;
∵AG⊥CG,OE⊥CG,BC⊥CG,
∴AG∥OE∥BC,而OA=OB,
∴GE=CE=4;
∵CE为⊙O的切线,
∴CE2=(CB-6)CB(切割线定理),
解得:CB=8或-2(舍去);
∵BE平分∠ABC,
∴
=
=
=
,
=
=
=
;
∵AD∥CE,
∴△CEF∽△AHF,△BCE∽△BDH;
∴
=
=
=
,
设CE=4m,则AH=5m,DH=3m;
∵△BCE∽△BDH,
∴
=
=
=
,
设BH=3x,则BE=4x,EH=x;
∵
=
,
∴EF=
x,BF=
x+x=
x,
∴
=
.
 解:(1)如图1,连接OE;
解:(1)如图1,连接OE;∵BE平分∠ABC,
∴∠OBE=∠CBE;而OB=OE,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE;
∵CG⊥BC,
∴∠CEB+∠CBE=90°,
∴∠CEB+∠OEB=90°,
即OE⊥CG,
∴CG为⊙O的切线.
(2)如图2,连接AD,交BE于点H;

∵CG⊥BC,AG∥BC,
∴∠GCB=90°;
又∵AB为⊙O的直径,
∴∠ADB=90°,
∴四边形ADCG为矩形,
∴AD=GC=8,
由勾股定理得:
BD2=AB2-AD2=100-64=36,
∴BD=6;
∵AG⊥CG,OE⊥CG,BC⊥CG,
∴AG∥OE∥BC,而OA=OB,
∴GE=CE=4;
∵CE为⊙O的切线,
∴CE2=(CB-6)CB(切割线定理),
解得:CB=8或-2(舍去);
∵BE平分∠ABC,
∴
| CF |
| AF |
| CB |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
| DH |
| AH |
| BD |
| AB |
| 6 |
| 10 |
| 3 |
| 5 |
∵AD∥CE,
∴△CEF∽△AHF,△BCE∽△BDH;
∴
| CE |
| AH |
| EF |
| FH |
| CF |
| AF |
| 4 |
| 5 |
设CE=4m,则AH=5m,DH=3m;
∵△BCE∽△BDH,
∴
| BH |
| BE |
| DH |
| CE |
| 3m |
| 4m |
| 3 |
| 4 |
设BH=3x,则BE=4x,EH=x;
∵
| EF |
| FH |
| 4 |
| 5 |
∴EF=
| 4 |
| 9 |
| 5 |
| 9 |
| 14 |
| 9 |
∴
| EF |
| BF |
| 2 |
| 7 |
点评:该题以圆为载体,以切线的判定、圆周角定理的推论、勾股定理等重要几何知识点的考查为核心构造而成;解题的关键是灵活运用有关知识点来分析、判断、推理或解答.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
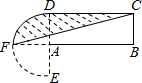 设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.
设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.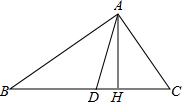 如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.
如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长. 已知:如图,AD∥BE∥CF.若AB=4,BC=6,DE=5,求DF.
已知:如图,AD∥BE∥CF.若AB=4,BC=6,DE=5,求DF.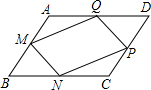 已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.
已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.