题目内容
直线y=
x+
与x轴相交于点A,与y轴相交于点B,以线段AB为一边在第二象限内作等边△ABC.
(1)求点C的坐标;
(2)设线段CD是△ABC的角平分线,求线段CD的解析式与定义域.
| 3 |
| 3 |
(1)求点C的坐标;
(2)设线段CD是△ABC的角平分线,求线段CD的解析式与定义域.
考点:待定系数法求一次函数解析式,等边三角形的性质
专题:
分析:(1)根据函数的关系式我们可求出A,B两点的坐标为(-1,0),(0,
),OA=1,OB=
,因此∠ABO=30°,因为三角形CAB是个等边三角形,因此∠CAB=60°,那么CB⊥OB,C点的纵坐标就是B点的纵坐标,如果求出CB的长那么就能求出C点的坐标了,根据BC=AB,有OA、OB的长,根据勾股定理我们可求出AB的长,也就求出BC的长,那么C点的坐标就求出来了.
(2)根据等边三角形角平分线的性质,可知CD⊥AB,根据直线y=
x+
即可得出直线CD的斜率,设直线CD为y=-
x+b,代入C的坐标即可求得线段CD的解析式;
| 3 |
| 3 |
(2)根据等边三角形角平分线的性质,可知CD⊥AB,根据直线y=
| 3 |
| 3 |
| ||
| 3 |
解答: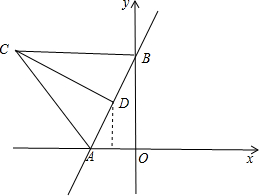 解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,
解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,
),
那么OA=1,OB=
,直角三角形ABO中,AB=
=2,∠ABO=30°,
根据三角形ABC是个等边三角形,因此∠CBA=60°.∠CBO=∠CBA+∠ABO=90°,
因此C点的纵坐标应该和A点相同,
∵AC=AB=BC,
∴BC=AB=2,
那么C点的坐标为(-2,2).
(2)∵线段CD是△ABC的角平分线,
∴直线CD垂直平分AB,
∴设这条直线CD为y=-
x+b,
将C点的坐标代入这条直线中得:-
×(-2)+b=2,b=
,
因此这条线段CD的解析式是y=-
x+
(-2≤x≤-
);
 解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,
解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,| 3 |
那么OA=1,OB=
| 3 |
| OA2+OB2 |
根据三角形ABC是个等边三角形,因此∠CBA=60°.∠CBO=∠CBA+∠ABO=90°,
因此C点的纵坐标应该和A点相同,
∵AC=AB=BC,
∴BC=AB=2,
那么C点的坐标为(-2,2).
(2)∵线段CD是△ABC的角平分线,
∴直线CD垂直平分AB,
∴设这条直线CD为y=-
| ||
| 3 |
将C点的坐标代入这条直线中得:-
| ||
| 3 |
6-2
| ||
| 3 |
因此这条线段CD的解析式是y=-
| ||
| 3 |
6-2
| ||
| 3 |
| 1 |
| 2 |
点评:本题综合考查了一次函数和直角三角形的应用,本题中利用直角三角形来求线段的长,从而得出点的坐标是解题的基本思路.

练习册系列答案
相关题目
下列事件中,是必然事件的是( )
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
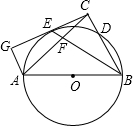 如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.
如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC. 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号): 从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,
从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,