题目内容
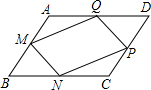 已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.
已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:根据平行四边形的对边相等可得AB=CD,BC=AD,对角相等可得∠A=∠C,然后求出AQ=CN,再利用“边角边”证明△AMQ和△CPN全等,根据全等三角形对应边相等可得MQ=PN,同理可证MN=PQ,然后根据两组对边分别相等的四边形是平行四边形证明四边形MNPQ是平行四边形,再根据平行四边形的对边平行证明即可.
解答:证明:在?ABCD中,AB=CD,BC=AD,∠A=∠C,
∵BN=DQ,
∴AD-DQ=BC-BN,
即AQ=CN,
在△AMQ和△CPN中,
,
∴△AMQ≌△CPN(SAS),
∴MQ=PN,
同理可证MN=PQ,
∴四边形MNPQ是平行四边形,
∴MN∥QP.
∵BN=DQ,
∴AD-DQ=BC-BN,
即AQ=CN,
在△AMQ和△CPN中,
|
∴△AMQ≌△CPN(SAS),
∴MQ=PN,
同理可证MN=PQ,
∴四边形MNPQ是平行四边形,
∴MN∥QP.
点评:本题考查了平行四边形的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键,难点在于求出三角形全等的对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
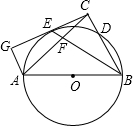 如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.
如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC. 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号): 如图,一艘船每小时35海里的速度向东北方向(北偏东45°)航行,在A处观测灯塔C在船的北偏东74°方向,航行了12分钟后到达B处,这时灯塔C恰好在船的正东方向,已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗,为什么?(参考数据:tan29°≈0.50,sin29°≈0.48,cos29°≈0.87)
如图,一艘船每小时35海里的速度向东北方向(北偏东45°)航行,在A处观测灯塔C在船的北偏东74°方向,航行了12分钟后到达B处,这时灯塔C恰好在船的正东方向,已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗,为什么?(参考数据:tan29°≈0.50,sin29°≈0.48,cos29°≈0.87)