题目内容
已知直线m、n是相交线,且直线l1⊥m,直线l2⊥n.求证:直线l1与l2必相交.
考点:反证法,相交线,垂线
专题:证明题
分析:假设直线l1与l2不相交,则两直线平行,即可证得m∥n,与已知矛盾,从而证得.
解答:证明:假设直线l1与l2不相交,则两直线平行.
∵l1∥l2,线l1⊥m,直线l2⊥n.
∴m∥n,
与直线m、n是相交线相矛盾.
则l1和l2平行错误,则直线l1与l2必相交.
∵l1∥l2,线l1⊥m,直线l2⊥n.
∴m∥n,
与直线m、n是相交线相矛盾.
则l1和l2平行错误,则直线l1与l2必相交.
点评:本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
相关题目
下列事件中,是必然事件的是( )
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
 下列形状的纸片,经过折叠可以围成一个棱柱的是
下列形状的纸片,经过折叠可以围成一个棱柱的是 如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.
如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.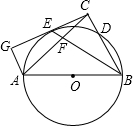 如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.
如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.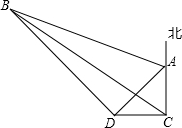 一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).