题目内容
18. 如图,在△ABC中,∠C=90°,∠B=20°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于P,连接AP并延长交BC于点D,则∠ADB=125°.
如图,在△ABC中,∠C=90°,∠B=20°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于P,连接AP并延长交BC于点D,则∠ADB=125°.
分析 根据角平分线的作法可得AD平分∠CAB,再根据三角形内角和定理可得∠ADB的度数.
解答 解:由题意可得:AD平分∠CAB,
∵∠C=90°,∠B=20°,
∴∠CAB=70°,
∴∠CAD=∠BAD=35°,
∴∠ADB=180°-20°-35°=125°.
故答案为:125°.
点评 此题主要考查了角平分线的作法以及角平分线的性质,熟练根据角平分线的性质得出∠ADB度数是解题关键.

练习册系列答案
相关题目
6.如图所示四个图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
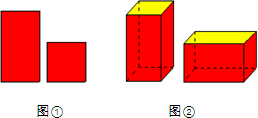 如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.
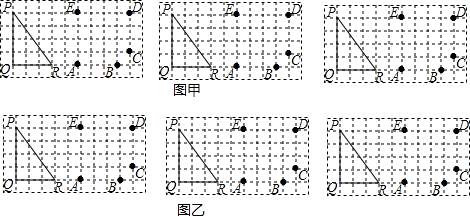
如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个. 如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(1,2).
如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(1,2).