题目内容
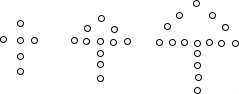
10．
如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是（1，2）．
分析 先根据旋转的性质得到点A的对应点为点A′，点B的对应点为点B′，再根据旋转的性质得到旋转中心在线段AA′的垂直平分线，也在线段BB′的垂直平分线，即两垂直平分线的交点为旋转中心．
解答 
解：∵将△ABC以某点为旋转中心，顺时针旋转90°得到△A′B′C′，
∴点A的对应点为点A′，点C的对应点为点C′，
作线段AA′和CC′的垂直平分线，它们的交点为P（1，2），
∴旋转中心的坐标为（1，2）．
故答案为：（1，2）
点评 本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，∠C=90°，∠B=20°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB=125°．
15．下列计算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （-2a）3=-6a3 | C． | （a2b）3=a5b2 | D． | （-a）6÷（-a）2=a4 |
19．在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆．在看不见图形的情况下随机摸出1张，是中心对称图形的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |