题目内容
3.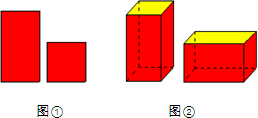 如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.
如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.
分析 设做竖式和横式的两种无盖纸盒分别为x个、y个,然后根据所需长方形纸板和正方形纸板的张数列出方程组解答即可.
解答 解:设做竖式和横式的两种无盖纸盒分别为x个、y个,根据题意得
$\left\{\begin{array}{l}{4x+3y=250}\\{x+2y=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=30}\end{array}\right.$,
40+30=70.
答:竖式和横式纸盒一共可做70个.
故答案为:70.
点评 本题考查了二元一次方程组的应用,根据系数的特点,观察出所需两种纸板的张数的和正好是5的倍数是解题的关键,也是解题的突破口.

练习册系列答案
相关题目
11. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )| A. | 7:00 | B. | 7:10 | C. | 7:25 | D. | 7:35 |
15.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (-2a)3=-6a3 | C. | (a2b)3=a5b2 | D. | (-a)6÷(-a)2=a4 |
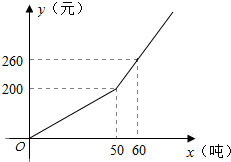 已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图. 如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16.
如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16. 如图,在△ABC中,∠C=90°,∠B=20°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于P,连接AP并延长交BC于点D,则∠ADB=125°.
如图,在△ABC中,∠C=90°,∠B=20°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于P,连接AP并延长交BC于点D,则∠ADB=125°. 如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD顶点在y=$\frac{1}{x}$上,且S矩形ABCD=2$\sqrt{5}$,则A的坐标xA=$\frac{\sqrt{5}+1}{2}$,yA=$\frac{\sqrt{5}-1}{2}$.