题目内容
设二次函数y=x2+(a-2)x-2a+3的图象为C,函数y=ax的图象为l.
(1)当a=3时,求C与l的交点坐标;
(2)求证图象C恒过定点,并求出这个定点.
(3)若图象C恒在图象l的上方,求实数a的取值范围.
(1)当a=3时,求C与l的交点坐标;
(2)求证图象C恒过定点,并求出这个定点.
(3)若图象C恒在图象l的上方,求实数a的取值范围.
考点:二次函数与不等式(组),二次函数图象上点的坐标特征
专题:
分析:(1)将a的值代入求出两函数解析式,再联立两函数解析式求解即可;
(2)整理成关于a的形式,再根据恒过定点与a的值无关求出x的值,然后求出y的值,再写出定点坐标即可;
(3)求出两函数图象没有交点时的a的取值范围即可.
(2)整理成关于a的形式,再根据恒过定点与a的值无关求出x的值,然后求出y的值,再写出定点坐标即可;
(3)求出两函数图象没有交点时的a的取值范围即可.
解答:解:(1)a=3时,y=x2+x-3,y=3x,
联立
,
解得
,
,
所以,C与l的交点坐标为(-1,-3),(3,9);
(2)y=x2+(a-2)x-2a+3=x2+a(x-2)-2x+3,
∵图象C恒过定点,
∴x-2=0,
∴x=2,
y=22-2×2+3=3,
∴函数图象C恒过定点(2,3);
(3)联立两函数解析式消掉y得,x2+(a-2)x-2a+3=ax,
整理得,x2-2x-2a+3=0,
∵图象C恒在图象l的上方,
∴方程没有实数解,
∴△=(-2)2-4×(-2a+3)<0,
解得a<1,
∴实数a的取值范围是a<1.
联立
|
解得
|
|
所以,C与l的交点坐标为(-1,-3),(3,9);
(2)y=x2+(a-2)x-2a+3=x2+a(x-2)-2x+3,
∵图象C恒过定点,
∴x-2=0,
∴x=2,
y=22-2×2+3=3,
∴函数图象C恒过定点(2,3);
(3)联立两函数解析式消掉y得,x2+(a-2)x-2a+3=ax,
整理得,x2-2x-2a+3=0,
∵图象C恒在图象l的上方,
∴方程没有实数解,
∴△=(-2)2-4×(-2a+3)<0,
解得a<1,
∴实数a的取值范围是a<1.
点评:本题考查了二次函数与不等式组,二次函数图象上点对点坐标特征,难点在于理解(2)恒过定点与a的值无关,(3)根据二次函数与一次函数的性质判断出两个函数没有交点时的情况即为所求.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
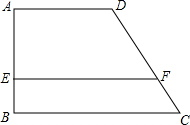 如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角A,B处均为直角,草地中间另有一条水泥直道EF垂直于AB于点E.若AE=a米,EB=b米,DF=c米,你能求出CF的长吗?
如图所示是一块形状为四边形的草地,周围均为水泥直道,两个拐角A,B处均为直角,草地中间另有一条水泥直道EF垂直于AB于点E.若AE=a米,EB=b米,DF=c米,你能求出CF的长吗? 如图所示,点A(1,4),点B(3,-1),点C(-4,-2),求以A、B、C三点为顶点的三角形的面积,并计算
如图所示,点A(1,4),点B(3,-1),点C(-4,-2),求以A、B、C三点为顶点的三角形的面积,并计算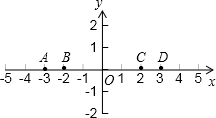
 如图,已知∠AOB=α,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠A0A2,…,OAn平分∠A0An-1,则∠AOAn的大小为
如图,已知∠AOB=α,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠A0A2,…,OAn平分∠A0An-1,则∠AOAn的大小为 如图,在?ABCD中,点E在CD上,点F在BC上,且BE=DF,BE、DF相交于点G,连接AG,求证:AG平分∠BGD.
如图,在?ABCD中,点E在CD上,点F在BC上,且BE=DF,BE、DF相交于点G,连接AG,求证:AG平分∠BGD.