题目内容
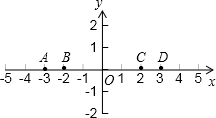
如图所示,A、B、C、D四点都在x轴上,C、D两点的横坐标分别为2,3,线段CD=1;B、D两点的横坐标分别为-2,3,线段BD=5;A、B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1<x2),那么线段MN的长为多少?
(2)如果y轴上有两点P(0,y1),Q(0,y2)(y1<y2),那么线段PQ的长为多少?
(3)如果|a|=3,b=2,且有A(a,0),B(b,0),那么线段AB的长为多少?
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1<x2),那么线段MN的长为多少?
(2)如果y轴上有两点P(0,y1),Q(0,y2)(y1<y2),那么线段PQ的长为多少?
(3)如果|a|=3,b=2,且有A(a,0),B(b,0),那么线段AB的长为多少?

考点:坐标与图形性质
专题:
分析:(1)根据已知条件可知,x轴上两点之间的距离等于这两点横坐标差的绝对值,依此可得线段MN的长;
(2)y轴上有两点之间的距离等于这两点纵坐标差的绝对值,依此可得线段PQ的长;
(3)先由|a|=3,得出a=±3,再根据x轴上两点之间的距离等于这两点横坐标差的绝对值即可求出线段AB的长.
(2)y轴上有两点之间的距离等于这两点纵坐标差的绝对值,依此可得线段PQ的长;
(3)先由|a|=3,得出a=±3,再根据x轴上两点之间的距离等于这两点横坐标差的绝对值即可求出线段AB的长.
解答:解:(1)∵x轴上有两点M(x1,0),N(x2,0)(x1<x2),
∴线段MN=|x1-x2|=x2-x1;
(2)∵y轴上有两点P(0,y1),Q(0,y2)(y1<y2),
∴线段PQ=|y1-y2|=y2-y1;
(3)∵|a|=3,
∴a=±3,
∴A(±3,0),B(2,0),
∴线段AB=|±3-2|=1或5.
∴线段MN=|x1-x2|=x2-x1;
(2)∵y轴上有两点P(0,y1),Q(0,y2)(y1<y2),
∴线段PQ=|y1-y2|=y2-y1;
(3)∵|a|=3,
∴a=±3,
∴A(±3,0),B(2,0),
∴线段AB=|±3-2|=1或5.
点评:本题考查了坐标与图形性质,两点间的距离,正确理解题意利用数形结合是解决本题的关键.

练习册系列答案
相关题目
抛物线y=2x2-3的顶点在( )
| A、x轴上 | B、y轴上 |
| C、第一象限 | D、第二象限 |
 如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=120m,则A、B两点之间距离为
如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=120m,则A、B两点之间距离为
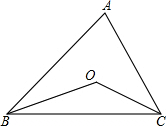 如图,点O是△ABC两内角平分线的交点
如图,点O是△ABC两内角平分线的交点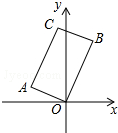 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是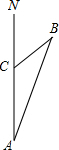 一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离.
一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离.