题目内容
 如图所示,点A(1,4),点B(3,-1),点C(-4,-2),求以A、B、C三点为顶点的三角形的面积,并计算
如图所示,点A(1,4),点B(3,-1),点C(-4,-2),求以A、B、C三点为顶点的三角形的面积,并计算| S△ADE |
| S△ABC |
考点:坐标与图形性质,三角形的面积
专题:
分析:如图,三角形ABC的面积等于矩形CFGH的面积减去三个小三角形的面积;利用待定系数法分别求出直线AB、AC的解析式,再求出D、E的坐标,得到DE的长,然后根据三角形面积公式求出△ADE的面积,进而求出
.
| S△ADE |
| S△ABC |
解答: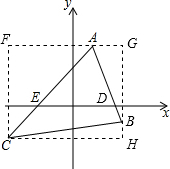 解:如图,
解:如图,
S△ABC=S矩形CFGH-S△AFC-S△BAG-S△CBH
=6×7-
×6×5-
×2×5-
×7×1
=
.
设直线AB的解析式为y=kx+b,
∵点A(1,4),点B(3,-1),
∴
,解得
,
∴直线AB的解析式为y=-
x+
,
∴当y=0时,x=
,
∴D(
,0).
设直线AC的解析式为y=mx+n,
∵点A(1,4),点C(-4,-2),
∴
,解得
,
∴直线AC的解析式为y=
x+
,
∴当y=0时,x=-
,
∴D(-
,0),
∴DE=
-(-
)=
,
∴S△ADE=
×
×4=
,
∴
=
=
.
 解:如图,
解:如图,S△ABC=S矩形CFGH-S△AFC-S△BAG-S△CBH
=6×7-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 37 |
| 2 |
设直线AB的解析式为y=kx+b,
∵点A(1,4),点B(3,-1),
∴
|
|
∴直线AB的解析式为y=-
| 5 |
| 2 |
| 13 |
| 2 |
∴当y=0时,x=
| 13 |
| 5 |
∴D(
| 13 |
| 5 |
设直线AC的解析式为y=mx+n,
∵点A(1,4),点C(-4,-2),
∴
|
|
∴直线AC的解析式为y=
| 6 |
| 5 |
| 14 |
| 5 |
∴当y=0时,x=-
| 7 |
| 3 |
∴D(-
| 7 |
| 3 |
∴DE=
| 13 |
| 5 |
| 7 |
| 3 |
| 74 |
| 15 |
∴S△ADE=
| 1 |
| 2 |
| 74 |
| 15 |
| 148 |
| 15 |
∴
| S△ADE |
| S△ABC |
| ||
|
| 8 |
| 15 |
点评:本题考查了三角形的面积、坐标与图形性质、待定系数法求直线的解析式,难度适中.将所求的三角形面积转化为矩形的面积与直角三角形的面积的差是求三角形ABC面积的关键,求出D、E的坐标是求三角形ADE面积的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
抛物线y=2x2-3的顶点在( )
| A、x轴上 | B、y轴上 |
| C、第一象限 | D、第二象限 |
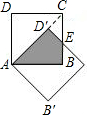 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
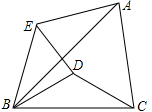 如图,△ABC中,AC=3,分别以BC、AB为底边作顶角为120°的等腰△BDC和△AEB,D在△ABC内,E在△ABC外,那么ED的长等于( )
如图,△ABC中,AC=3,分别以BC、AB为底边作顶角为120°的等腰△BDC和△AEB,D在△ABC内,E在△ABC外,那么ED的长等于( )
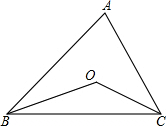 如图,点O是△ABC两内角平分线的交点
如图,点O是△ABC两内角平分线的交点