题目内容
19.对于任意的有理数a,方程2x2+(a+1)x-(3a2-4a+b)=0的根总是有理数,则b的值为( )| A. | 1 | B. | -1 | C. | 2 | D. | 0 |
分析 首先得出△=(a+1)2+8(3a2-4a+b)=(5a-3)2+8b-8≥0,进而利用b=1,-1,2,0时求出方程可能存在的解,进而得出答案.
解答 解:∵方程的△=(a+1)2+8(3a2-4a+b)=(5a-3)2+8b-8≥0,
∴当8b-8≥0时,
必定△≥0,即方程必有实根,
∴b≥1,当b=1时,3a2-4a+1=(3a-1)(a-1),
∴十字因式分解得方程为(x-a+1)(2x+3a-1)=0,
∴b=1成立,
当b=2时,3a2-4a+b=3a2-4a+2不能因式分解,
∴方程有可能为无理数解,
同理可得b=-1以及0时,方程有可能为无理数解,
故b的值为1.
故选:A.
点评 此题主要考查了一元二次方程的整数根与有理根,在一元二次方程中,运用方程的判别式和因式分解是解决方程有理根和整数根重要工具.

练习册系列答案
相关题目
4.已知圆O的圆心到直线L的距离为3,若圆上有且只有2个点到L的距离为2,则半径r的取值范围是( )
| A. | r=3 | B. | 1<r<3 | C. | 1<r<5 | D. | 1≤r≤5 |
 如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.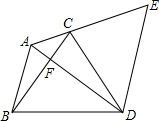 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.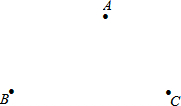 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?