题目内容
14.已知x1,x2是方程x2-(k-2)x+k2+3k+5=0的实数根(x1,x2可相等)(1)证明方程的两根都小于0;
(2)当实数k取何值时x12+x22最大?并求出最大值.
分析 (1)根据判别式的意义得到△=(k-2)2-4(k2+3k+5)≥0,解此不等式得到-4≤k≤-$\frac{4}{3}$,再由根与系数的关系得x1+x2=k-2,x1x2=k2+3k+5,利用k的取值范围有x1+x2=k-2<0,x1x2=k2+3k+5>0,于是利用有理数的性质即可判断方程的两根都小于0;
(2)利用完全平方公式得到x12+x22=(x1+x2)2-2x1x2=(k-2)2-2(k2+3k+5)=-(k+5)2+19,然后根据二次函数的最值问题求解.
解答 (1)证明:∵△=(k-2)2-4(k2+3k+5)≥0,
∴-4≤k≤-$\frac{4}{3}$,
∵x1+x2=k-2,x1x2=k2+3k+5,
∴x1+x2=k-2<0,x1x2=k2+3k+5>0,
∴方程的两根都小于0;
(2)解:x12+x22=(x1+x2)2-2x1x2=(k-2)2-2(k2+3k+5)=-k2-10k-6=-(k+5)2+19,
∵-4≤k≤-$\frac{4}{3}$,
∴k=-4时,x12+x22有最大值,最大值为-(-4+5)2+19=18.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,△ABC的三条中线AD,BE,CF交于点O,且AD=5,则AO=$\frac{5}{3}$.
如图,△ABC的三条中线AD,BE,CF交于点O,且AD=5,则AO=$\frac{5}{3}$.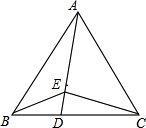 如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.
如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.