题目内容
11.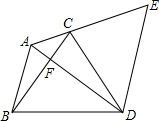 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
分析 过D作DM⊥AE,根据旋转的性质得到AB=CE=5,AD=DE,∠ADE=60°,于是得到△ADE是等边三角形,推出AD=DE=AE=AC+CE=8,由于DM⊥AE,得到AM=4,MD=4$\sqrt{3}$,求出CD=7,由△BCD是等边三角形,得出BC=CD=7,由于∠BAC=120°,∠DAE=60°,得到AF是∠BAC的角平分线,于是得到$\frac{AB}{AC}=\frac{BF}{CF}$,解得BF=$\frac{5}{3}CF$,于是求得结论.
解答 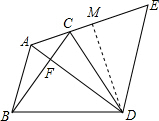 解:过D作DM⊥AE,根据旋转的性质得:AB=CE=5,AD=DE,∠ADE=60°,
解:过D作DM⊥AE,根据旋转的性质得:AB=CE=5,AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∴AD=DE=AE=AC+CE=8,
∵DM⊥AE,
∴AM=4,MD=4$\sqrt{3}$,
∴CM=1,
∴CD=7,
∵△BCD是等边三角形,
∴BC=CD=7,
∵∠BAC=120°,∠DAE=60°,
∴∠DAE=∠BAD,
∴AF是∠BAC的角平分线,
∴$\frac{AB}{AC}=\frac{BF}{CF}$,
∴BF=$\frac{5}{3}CF$,
∵BF+CF=7,
∴CF=$\frac{21}{8}$.
故答案为:$\frac{21}{8}$.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目