题目内容
4.某商场两天销售甲、乙两种商品的记录如表,由于售货员字迹潦草,无法准确确认第二天的总金额的个位数字,只知道个位数是0或6,并且已知两种商品的销售价仅为整数.| 总数量(件) | 总金额 | ||
| 甲 | 乙 | ||
| 第一天 | 20 | 10 | 280 |
| 第二天 | 15 | 15 | 27x |
(2)若一件甲商品进价为7元,一件乙商品的进价为6元,某天共卖出40件,且两者总利润不低于100元,则至多销售乙商品多少件?
分析 1)通过理解题意可知:本题的等量关系是:第一天销售的甲商品的金额+第一天销售的乙商品的金额=280元;第二天销售的甲商品的金额+第二天销售的乙商品的金额=第二天的总金额,列方程组求解即可;
(2)由题意可知:甲产品的利润+乙产品的利润≥100,解不等式即可.
解答 解:(1)设甲、乙两种产品的单价分别为x元、y元,由题意得
$\left\{\begin{array}{l}{20x+10y=280}\\{15x+15y=270}\end{array}\right.$或$\left\{\begin{array}{l}{20x+10y=280}\\{15x+15y=276}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=10}\\{y=8}\end{array}\right.$或$\left\{\begin{array}{l}{x=9.6}\\{y=8.8}\end{array}\right.$(不合题意,舍去).
答:甲、乙两种产品的单价分别为10元、8元.
(2)设销售乙商品a件,则销售甲商品(40-x)件.依题意
(10-7)×(40-a)+(8-6)a≥100,
解得a≤20.
故至多销售乙商品20件.
点评 此题考查二元一次方程组和不等式组的实际运用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.

练习册系列答案
相关题目
15.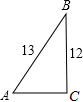 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )| A. | sinA=$\frac{12}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{5}{12}$ | D. | tanB=$\frac{12}{5}$ |
9.把一次函数y=-2x的图象向上平移3个单位长度,平移后,若y>0,则x的取值范围是( )
| A. | x>$\frac{3}{2}$ | B. | x<$\frac{3}{2}$ | C. | x>3 | D. | x<3 |
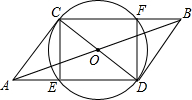 如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.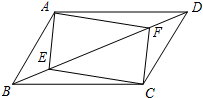 如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.