题目内容
14.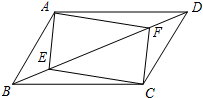 如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?
(3)若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.
分析 (1)连接AC交BD于点O,由平行四边形的性质得出OA=OC,OE=OF,再证出OB=OD,即可得出结论;
(2)由菱形的性质得出AC⊥BD,即可得出结论;
(3)由矩形的性质得出OA=OC=OE=OF,证出OB=OD,AC<BD,得出四边形ABCD是平行四边形,不是矩形.
解答 (1)证明:连接AC交BD于点O,如图所示: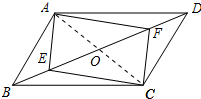
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形;
(2)解:理由如下:
∵四边形AECF是菱形,
∴AC⊥BD,
由(1)知,四边形ABCD是平行四边形;
∴四边形ABCD是菱形;
(3)解:四边形ABCD不是矩形;理由如下:
∵四边形AECF是矩形,
∴OA=OC,OE=OF,AC=EF,
∴OA=OC=OE=OF,
∵BE=DF,
∴OB=OD,
∴AC<BD,
∴四边形ABCD是平行四边形,不是矩形.
点评 本题考查了平行四边形的性质与判定、菱形的性质与判定、矩形的性质;熟练掌握平行四边形、矩形、菱形的性质、并能进行推理论证是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.某商场两天销售甲、乙两种商品的记录如表,由于售货员字迹潦草,无法准确确认第二天的总金额的个位数字,只知道个位数是0或6,并且已知两种商品的销售价仅为整数.
(1)请求出甲、乙两种商品的销售价格各为多少?
(2)若一件甲商品进价为7元,一件乙商品的进价为6元,某天共卖出40件,且两者总利润不低于100元,则至多销售乙商品多少件?
| 总数量(件) | 总金额 | ||
| 甲 | 乙 | ||
| 第一天 | 20 | 10 | 280 |
| 第二天 | 15 | 15 | 27x |
(2)若一件甲商品进价为7元,一件乙商品的进价为6元,某天共卖出40件,且两者总利润不低于100元,则至多销售乙商品多少件?
5.要调查某校九年级550名学生周日的睡眠时间,下列调查对象选取最合适的是( )
| A. | 选取该校一个班级的学生 | B. | 随机选取该校50名九年级学生 | ||
| C. | 选取该校50名九年级女生 | D. | 选取该校50名男生 |
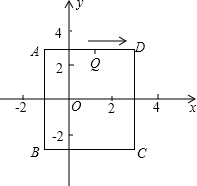 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$).
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$).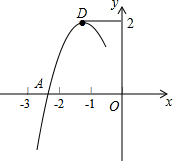 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: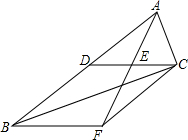 如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.