题目内容
 如图,△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,△BOM的面积为2,则四边形MCNO的面积为
如图,△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,△BOM的面积为2,则四边形MCNO的面积为考点:三角形的面积
专题:
分析:根据“三角形的中线将三角形分为面积相等的两个三角形”得到S△ABM=S△ABN=
S△ABC=6,然后结合图形来求四边形MCNO的面积.
| 1 |
| 2 |
解答: 解:如图,∵△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,
解:如图,∵△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,
∴S△ABM=S△ABN=
S△ABC=6.
又∵S△ABM-S△BOM=S△AOB,△BOM的面积为2,
∴S△AOB=2,
∴S四边形MCNO=S△ABC-S△ABN-S△AOB=12-6-2=4.
故答案是:4.
 解:如图,∵△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,
解:如图,∵△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为12,∴S△ABM=S△ABN=
| 1 |
| 2 |
又∵S△ABM-S△BOM=S△AOB,△BOM的面积为2,
∴S△AOB=2,
∴S四边形MCNO=S△ABC-S△ABN-S△AOB=12-6-2=4.
故答案是:4.
点评:本题考查了三角形的面积.解答该题时,需要利用“数形结合”是数学思想.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知点P(0,a)在y轴的负半轴上,则点Q(a2,-a+1)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=2:3,BD平分∠ABC,点F在BC上,∠CDF=30°,∠ABD=35°.
如图,在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=2:3,BD平分∠ABC,点F在BC上,∠CDF=30°,∠ABD=35°.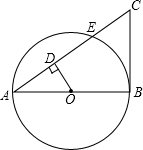 如图,AB为⊙O的直径,OD⊥AC于D,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,OD⊥AC于D,AC交⊙O于点E,D为AC上一点,∠AOD=∠C. 假如小蚂蚁在如图的3×3方格的地砖上爬行,它最终停在黑砖上的概率为
假如小蚂蚁在如图的3×3方格的地砖上爬行,它最终停在黑砖上的概率为 如图,?ABCD中,DE平分∠ADC交边BC于点E,AD=9,AB=6,则BE=
如图,?ABCD中,DE平分∠ADC交边BC于点E,AD=9,AB=6,则BE=