Question

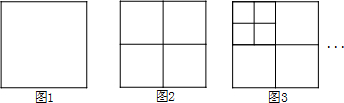
将正方形如图1作如下操作：第1次：分别连结各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，第4次操作得到的正方形个数是

 

个；若要得到2001个正方形，则需要操作的次数是

 

次；第n次操作得到的正方形个数是

 

个（n为正整数）．

Answer 1

考点：规律型：图形的变化类

专题：

分析：根据正方形的个数变化可设第n次得到2013个正方形，则4n+1=2013，求出即可．

解答：解：∵第1次：分别连接各边中点如图2，得到4+1=5个正方形；
第2次：将图2左上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形…，
第4次得到：4×4+1=17个正方形；
以此类推，根据以上操作，第n次得到4n+1个正方形，
根据以上操作，若第n次得到2001个正方形，则4n+1=2001，
解得：n=500．
故答案为：17，500，4n+1．

点评：此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键．