题目内容
12.如图,在10×6的正方形网格中,每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
(1)在图中以AB为边画Rt△ABC,点C在小正方形的格点上,使∠BAC=90°,且tan∠ACB=$\frac{2}{3}$;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的格点上,使∠CBD=45°,连接CD,直接写出线段CD的长.
分析 (1)如图,作∠BAC=90°,且边AC=3$\sqrt{2}$,才能满足条件;
(2)作DE=2,连接DF,则△DEF是以EF为边且面积为3的三角形,连接BD,CD,则∠CBD=45°.
解答  解:(1)如图,
解:(1)如图,
由勾股定理得:AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,BC=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,
∴AB2+AC2=(2$\sqrt{2}$)2+(3$\sqrt{2}$)2=26,
BC2=($\sqrt{26}$)2=26,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
tan∠ACB=$\frac{AB}{AC}$=$\frac{2\sqrt{2}}{3\sqrt{2}}$=$\frac{2}{3}$;
(2)如图,∵S△DEF=$\frac{1}{2}$×2×3=3,
∵BC=$\sqrt{26}$,CD=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,BD=$\sqrt{{4}^{2}+{6}^{2}}$=$\sqrt{52}$,
∴BC2+CD2=52,BD2=52,
∴BC2+CD2=BD2,
∴∠BCD=90°,BC=CD,
∴∠CBD=45°,
∴CD=$\sqrt{26}$.
点评 本题是三角形的作图题,考查了等腰直角三角形的性质和判定及勾股定理及其逆定理的运用,并按条件作出三角形;本题的关键是熟练掌握勾股定理及其逆定理.

练习册系列答案
相关题目
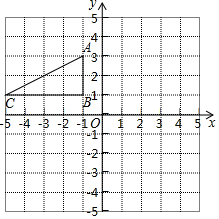 △ABC在平面直角坐标系中的位置如图所示:将△ABC的横坐标不变,纵坐标乘以-1得到△A1B1C1画出图形,并说明所得的图形与原图形有什么关系?并写出A1、B1、C1的坐标.
△ABC在平面直角坐标系中的位置如图所示:将△ABC的横坐标不变,纵坐标乘以-1得到△A1B1C1画出图形,并说明所得的图形与原图形有什么关系?并写出A1、B1、C1的坐标. 如图:点C是线段AB上的点,点D是线段BC的中点,若AC:BC=3:2,且AD=8,求线段AB的长.
如图:点C是线段AB上的点,点D是线段BC的中点,若AC:BC=3:2,且AD=8,求线段AB的长. 如图,正方形ABCD与正方形AEFG有公共顶点A,连接BE、CF,则线段BE:CF的值是$\frac{\sqrt{2}}{2}$.
如图,正方形ABCD与正方形AEFG有公共顶点A,连接BE、CF,则线段BE:CF的值是$\frac{\sqrt{2}}{2}$.