Question

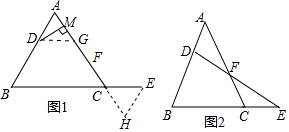
1．如图，正方形ABCD与正方形AEFG有公共顶点A，连接BE、CF，则线段BE：CF的值是$\frac{\sqrt{2}}{2}$．

Answer 1

分析 连接AC、CF、AF、DG．由△DAG≌△BAE，推出DG=BE，由△DAG∽△CAF，推出$\frac{DG}{CF}$=$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$，由此即可解决问题．

解答 解：连接AC、CF、AF、DG．

在正方形ABCD与正方形AEFG中，
∵AD=AB，AG=AE，∠DAB=∠GAE=90°，
∴∠DAG=∠BAE，
∴△DAG≌△BAE，
∴DG=BE，
∵∠DAC=∠GAF=45°，
∴∠DAG=∠CAF，
∵AC=$\sqrt{2}$AD，AF=$\sqrt{2}$AG，
∴$\frac{AD}{AC}$=$\frac{AG}{AF}$=$\frac{1}{\sqrt{2}}$，
∴△DAG∽△CAF，
∴$\frac{DG}{CF}$=$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$，
∴$\frac{BE}{CF}$=$\frac{\sqrt{2}}{2}$．

点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，正确寻找全等三角形或相似三角形解决问题，属于中考填空题中的压轴题．