题目内容
17.(1)化简($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$.(2)解方程组$\left\{\begin{array}{l}{3x+4y=19}\\{x-y=4}\end{array}\right.$.
分析 (1)根据分式的运算即可求出答案.
(2)根据方程组的解法即可求出答案.
解答 解:(1)原式=$\frac{-(x+y)}{x}$×$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=$\frac{y-x}{x}$
(2)由x-y=4可知:x=4+y
将x=4+y代入3x+4y=19,
∴3(4+y)+4y=19
∴y=1,
将y=1代入x=4+y,
∴x=5,
∴该方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
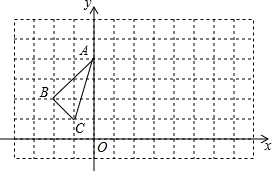
 如图,△ABC和△DBA在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置.
如图,△ABC和△DBA在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置.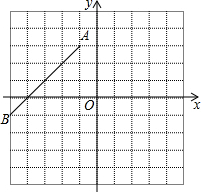 已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB,
已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB,