题目内容
9.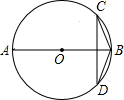 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
分析 连接AD,由AB是⊙O的直径,根据直径所对的圆周角是直角,即可求得∠ADB=90°,继而求得∠A的度数,然后由圆周角定理,求得∠BCD的度数.
解答  解:连接AD,
解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=56°,
∴∠A=90°-∠ABD=34°,
∴∠C=∠A=34°.
故选B.
点评 此题考查了圆周角定理与直角三角形的性质.此题比较简单,注意掌握辅助线的作法,注意直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.比较下列各组数的大小:
(1)$\sqrt{11}$与$\sqrt{5}$+$\sqrt{3}$;
(2)$\sqrt{15}$-$\sqrt{13}$与$\sqrt{13-\sqrt{11}}$.
(1)$\sqrt{11}$与$\sqrt{5}$+$\sqrt{3}$;
(2)$\sqrt{15}$-$\sqrt{13}$与$\sqrt{13-\sqrt{11}}$.
2.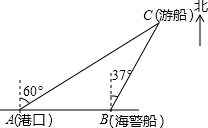 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )| A. | $\frac{1}{sin37°}$ | B. | $\frac{1}{cos37°}$ | C. | sin37° | D. | cos37° |
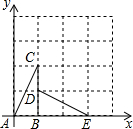 如图,在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,将△ABC绕点B顺时针旋转90°到△DBE
如图,在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,将△ABC绕点B顺时针旋转90°到△DBE 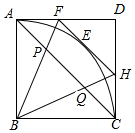 如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.
如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H. 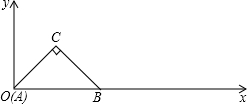 在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.
在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.