题目内容
18.比较下列各组数的大小:(1)$\sqrt{11}$与$\sqrt{5}$+$\sqrt{3}$;
(2)$\sqrt{15}$-$\sqrt{13}$与$\sqrt{13-\sqrt{11}}$.
分析 (1)先求出平方,作差比较平方的大小,即可解答;
(2)先计算出平方,作差比较大小,即可解答.
解答 解:(1)$(\sqrt{11})^{2}$=11,$(\sqrt{5}+\sqrt{3})^{2}=8+2\sqrt{15}$,
11-(8+2$\sqrt{15}$)=3-2$\sqrt{15}$<0,
∴$\sqrt{11}<\sqrt{5}+\sqrt{3}$.
(2)$(\sqrt{15}-\sqrt{13})^{2}=28-2\sqrt{13×15}$,$(\sqrt{13-\sqrt{11}})^{2}=13-\sqrt{11}$,
28-2$\sqrt{13×15}$-(13-$\sqrt{11}$)
=15$+\sqrt{11}-2\sqrt{13×15}$,
$(15+\sqrt{11})^{2}=225+11+30\sqrt{11}=236+30\sqrt{11}$,
$(2\sqrt{13×15})^{2}=4×13×15$=780,
236+30$\sqrt{11}$-780=30$\sqrt{11}$-544,
$(30\sqrt{11})^{2}=900×11=9900$,5442=296936,
∴30$\sqrt{11}$<544,
∴$\sqrt{15}-\sqrt{13}<\sqrt{13-\sqrt{11}}$
点评 本题考查了实数比较大小,解决本题的关键是计算各个代数式的平方,再作差比较大小.

练习册系列答案
相关题目
8.若正比例函数y=kx(k≠0)的图象经过点P(-2,3),则该函数的图象经过的点是( )
| A. | (3,-2) | B. | (1,-6) | C. | (2,-3) | D. | (-1,-6) |
9.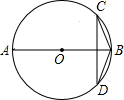 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
3.使二次根式$\sqrt{x-1}$的有意义的x的取值范围是( )
| A. | x>0 | B. | x>1 | C. | x≥1 | D. | x≠1 |
 (1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
(1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
