题目内容
1.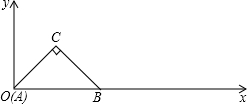 在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.
在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.
分析 由勾股定理求出AB,由题意得出点A经过的路线与x轴围成的图形是一个圆心角为135°,半径为$\sqrt{2}$的扇形,加上△ABC,再加上圆心角是90°,半径是1的扇形;由扇形的面积和三角形的面积公式即可得出结果.
解答 解:∵∠C=90°,AC=BC=1,
∴AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
根据题意得:$\sqrt{2}$△ABC绕点B顺时针旋转135°,BC落在x轴上;△ABC再绕点C顺时针旋转90°,AC落在x轴上,停止滚动;
∴点A的运动轨迹是:先绕点B旋转135°,再绕点C旋转90°;如图所示:
∴点A经过的路线与x轴围成的图形是:
一个圆心角为135°,半径为$\sqrt{2}$的扇形,加上△ABC,再加上圆心角是90°,半径是1的扇形;
∴点A经过的路线与x轴围成图形的面积
=$\frac{135×π×(\sqrt{2})^{2}}{360}$+$\frac{1}{2}$×1×1+$\frac{90×π×{1}^{2}}{360}$=π+$\frac{1}{2}$;
故答案为:π+$\frac{1}{2}$.
点评 本题考查了旋转的性质、扇形面积的计算公式;根据题意得出点A经过的路线与x轴围成的图形由三部分组成是解决问题的关键.

练习册系列答案
相关题目
9.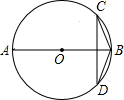 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
16.若代数式$\frac{\sqrt{2-x}}{1+x}$有意义,则x的取值范围是( )
| A. | x≥-2且x≠-1 | B. | x>-2且x≠-1 | C. | x≤2且x≠-1 | D. | x<2且x≠-1 |
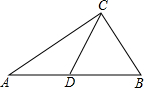 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,CD是AB边上的中线,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,CD是AB边上的中线,则CD的长是5. 如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.
如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.
 (1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
(1)计算:$\sqrt{8}$-(π-1)0-4sin45°;