题目内容
18.已知:$\frac{3x-4}{(x-1)(1-x)}$=$\frac{A}{x-1}$+$\frac{B}{x-2}$,则A=1和B=2.分析 把等式右边通分计算,再利用待定系数法可求得答案.
解答 解:
∵$\frac{A}{x-1}$+$\frac{B}{x-2}$=$\frac{A(x-2)}{(x-1)(x-2)}$+$\frac{B(x-1)}{(x-1)(x-2)}$=$\frac{(A+B)x-(2A+B)}{(x-1)(x-2)}$,
∴$\frac{3x-4}{(x-1)(1-x)}$=$\frac{(A+B)x-(2A+B)}{(x-1)(x-2)}$,
∴$\left\{\begin{array}{l}{A+B=3}\\{2A+B=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$,
故答案为:1;2.
点评 本题主要考查分式的加减运算,把等式的右边通分与左边化成同分母的分式是解题的关键.

练习册系列答案
相关题目
13.2,5,9,12,9,( )
| A. | 14 | B. | 6 | C. | -5 | D. | -9 |

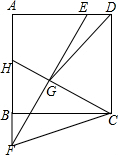 如图,正方形ABCD中,AB=8$\sqrt{5}$,E是AD边上一点,F是AB延长线上一点,且DE=BF,连接EF,G是EF的中点,延长CG交AB于点H,H恰好是AB的中点,连接DG,则DG的长是多少?
如图,正方形ABCD中,AB=8$\sqrt{5}$,E是AD边上一点,F是AB延长线上一点,且DE=BF,连接EF,G是EF的中点,延长CG交AB于点H,H恰好是AB的中点,连接DG,则DG的长是多少?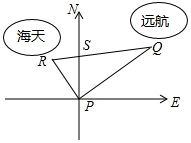 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{1}{2}$小时后相距10海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{1}{2}$小时后相距10海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
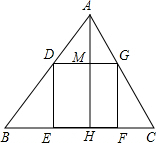 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知△ABC的边BC=15,高AH=10,求正方形DEFG的边长和面积.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知△ABC的边BC=15,高AH=10,求正方形DEFG的边长和面积.