��Ŀ����
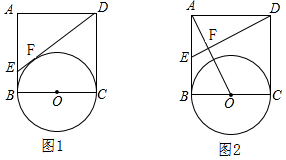
9����ͼ���ھ���ABCD��AD��AB���У�PΪBC���ϵ�һ�㣬AP=AD������P��PE��PA��CD��E������AE���ӳ���BC���ӳ�����F����1����֤����APE�ա�ADE��
��2����AB=3��CP=1������BP��CF�ij���
��3���ڣ�2���������£�����PD������MΪAP�ϵĶ��㣬NΪAD�ӳ����ϵĶ��㣬��PM=DN������MN��PD��G����MH��PD������ΪH�����ʵ�M��N���ƶ������У��߶�GH�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���GH�ij���

���� ��1�����жϳ���APE=��D=90�㣬���ɵó����ۣ�
��2�������CD=AB=3���������ù��ɶ������CE=$\frac{4}{3}$��DE=$\frac{5}{3}$���١�ABP�ס�PCE�����ɵó�BP=4���ɵó����ۣ�
��3�����жϳ�MI=DN�������жϳ���MGH�ա�NGD������ù��ɶ������ɵó����ۣ�
��� ��1��֤����
���ھ���ABCD�У���D=90�㣬��PE��PA��
���APE=��D=90�㣬
�֡�AP=AD��AE=AE��
���APE�ա�ADE
��2���ɡ�APE�ա�ADE��DE=PE
��AB=3��
��CD=AB=3
����Rt��PCE����CE=x����PE=3-x��
�ࣨ3-x��2=x2+12�����x=$\frac{4}{3}$
��CE=$\frac{4}{3}$��DE=$\frac{5}{3}$
�֡ߡ�B=��BCD=��APE=90��
���PEC+��CPE=90�㣬��APB+��CPE=90��
���PEC=��APB
���ABP�ס�PCE
��$\frac{BP}{AB}=\frac{CE}{CP}$����BP=4
����Rt��ABP��AP=AD=5��
�֡�AD��BC
��$\frac{CF}{AD}=\frac{CE}{DE}=\frac{4}{5}$
��CF=4
��3��û�б仯H
��ͼ2��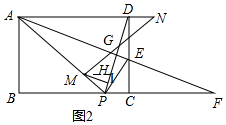
��MI��DN��PD��I
��AD=AP��MI��DN
���ADP=��APD����ADP=��MIP
���APD=��MIP
��MI=PM
�֡�MH��PD
��PH=HI
�֡�PM=DN
��MI=DN
���MGI=��DGN����IMG=��DNG��
���MGH�ա�NGD
��GI=GD
��GH=GI+IH=$\frac{1}{2}$PD
����Rt��ABP��PD=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
��GH=$\frac{\sqrt{10}}{2}$��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ�ȫ�������ε��ж������ʣ����������ε��ж������ʣ����ɶ������⣨1���Ĺؼ����жϳ�����APE=��D=90�㣬�⣨2���Ĺؼ������CE=$\frac{4}{3}$��DE=$\frac{5}{3}$���⣨3���Ĺؼ����жϳ�MI=DN��

| A�� | -22=4 | B�� | ��-2��3=8 | C�� | $\root{3}{64}$=4 | D�� | $\sqrt{4}=��2$ |
| A�� | 4 | B�� | 2$\sqrt{3}$ | C�� | $\sqrt{6}$ | D�� | $\sqrt{2}$ |
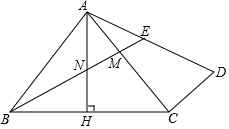 ��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬AH��BC�ڵ�H������C��CD��AC������AD����MΪAC��һ�㣬��AM=CD������BM��AH�ڵ�N����AD�ڵ�E��
��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬AH��BC�ڵ�H������C��CD��AC������AD����MΪAC��һ�㣬��AM=CD������BM��AH�ڵ�N����AD�ڵ�E��