题目内容
7.先化简再求值,(ab+1)(ab-2)+(a-2b)2+(a+2b)(-2b-a),其中a=$\frac{2}{3}$,b=-$\frac{3}{4}$.分析 首先计算乘方,再计算多项式乘以多项式,然后合并同类项,化简后,再代入a、b的值可得答案.
解答 解:原式=a2b2-ab-2+a2+4b2-4ab-2ab-a2-4b2-2ab,
=a2b2-9ab-2,
当a=$\frac{2}{3}$,b=-$\frac{3}{4}$时,
原式=$\frac{4}{9}$×$\frac{9}{16}$+9×$\frac{2}{3}$×$\frac{3}{4}$-2=$\frac{1}{4}$+$\frac{9}{2}$-2=$\frac{19}{4}$-2=$\frac{11}{4}$.
点评 此题主要考查了整式的混合运算--化简求值,关键是掌握先按运算顺序把整式化简,再把对应字母的值代入求整式的值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
17.下列运算正确的是( )
| A. | -22=4 | B. | (-2)3=8 | C. | $\root{3}{64}$=4 | D. | $\sqrt{4}=±2$ |
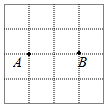 如图4×4的正方形网格每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数有( )
如图4×4的正方形网格每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数有( )